Примеры решения типовых задач. 1.Доказать, что данная функция задает скалярное произведение в ( − линейное пространство над полем
1. Доказать, что данная функция
Пример 1.
Решение. Далее положим для краткости
Остальные аксиомы скалярного произведения легко проверяются. Проверим, например, вторую аксиому:
Следовательно, данная функция задает скалярное произведение в пространстве 2. В гильбертовом пространстве Пример 1.
Решение. По определению проекции требуется найти такой вектор
Ясно, что это условие может выполняться для любых
Преобразуем эту систему:
Решая систему, получим Значит, проекция вектора
3. Доказать, что в указанном нормированном пространстве
Пример 1. Решение. Допустим противное, то есть что в
Но если
Подстановка этих данных в (1) приводит к противоречию. 4. Вычислить угол между векторами
Пример 1. Решение. По определению угол
Поскольку в нашем случае
то
5. Становится ли система векторов Пример 1.
Решение. Легко проверить, что
6. Для данного подмножества М гильбертова пространства
Пример 1. Решение. Заметим, что любую функцию
Пусть теперь
откуда следует, что Обратно, если Значит,
Пример 2.
Решение. Введем обозначение
Пусть
- одномерное подпространство, порожденное функцией
Следовательно,
|

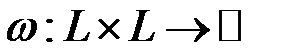 задает скалярное произведение в
задает скалярное произведение в  (
( − линейное пространство над полем
− линейное пространство над полем  ).
). ,
, .
. .Функция
.Функция  определена для любых
определена для любых  в силу неравенства
в силу неравенства .
. .
. .
. найти проекцию вектора
найти проекцию вектора  на заданное подпространство
на заданное подпространство  ,
,
 .
. , что
, что  , то есть
, то есть 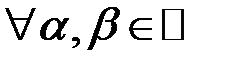
 .
.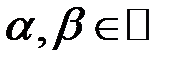 в том и только в том случае, если
в том и только в том случае, если
 ,
, ,
,
 .
. на подпространство
на подпространство 
 со стандартной нормой нельзя ввести скалярное произведение, порождающее эту норму.
со стандартной нормой нельзя ввести скалярное произведение, порождающее эту норму. .
.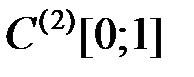 можноввести скалярное произведение, порождающее стандартную норму. Тогда (как и в любом предгильбертовом пространстве) должно выполняться равенство параллелограмма:
можноввести скалярное произведение, порождающее стандартную норму. Тогда (как и в любом предгильбертовом пространстве) должно выполняться равенство параллелограмма: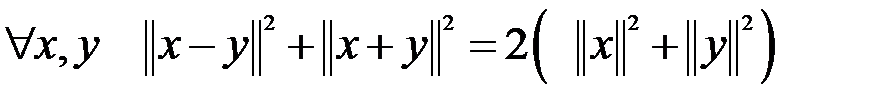 . (1)
. (1) , то легко подсчитать, что
, то легко подсчитать, что ,
,  ,
,  ,
,  .
. в пространстве
в пространстве  над
над  .
. ,
,  ,
,  .
. между ненулевыми векторами х и у удовлетворяет соотношениям
между ненулевыми векторами х и у удовлетворяет соотношениям .
. ,
, , а тогда искомый угол равен
, а тогда искомый угол равен  .
. после нормировки ортонормированным базисом пространства
после нормировки ортонормированным базисом пространства  , если
, если  (единица стоит на n -ном месте)?
(единица стоит на n -ном месте)? ,
, 
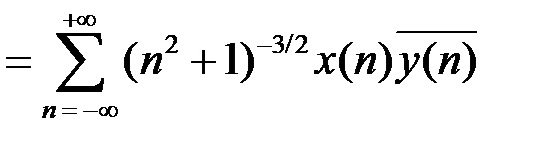 .
. для любых
для любых  (проверьте). Кроме того, система
(проверьте). Кроме того, система  обладает свойством максимальности. Действительно, возьмем
обладает свойством максимальности. Действительно, возьмем  и допустим, что
и допустим, что 
 . Тогда
. Тогда 
 . Отсюда
. Отсюда  , т. е.
, т. е.  . Итак, система
. Итак, система  максимальна. Значит, после нормировки
максимальна. Значит, после нормировки  станет ортонормированным базисом (почему?).
станет ортонормированным базисом (почему?). .
. ,
, 
 при
при  .
. можно представить в виде
можно представить в виде  , причем
, причем ,
, 
 . Тогда
. Тогда  , а так как
, а так как  , то
, то  . Значит,
. Значит,

 почти всюду на
почти всюду на  .
. почти всюду на
почти всюду на 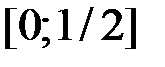 , то
, то  , то есть
, то есть  .
.
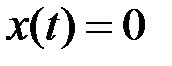 почти всюду при
почти всюду при 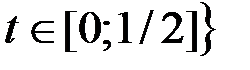 .
. ,
, 
 .
. . Тогда имеем
. Тогда имеем
 .
.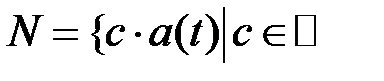
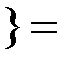

 . Тогда
. Тогда

 .
. , то есть
, то есть 
 .
.