Гильбертовы пространства и интегральные уравнения
Тема 5.1 Гильбертовы пространства. Основные понятия
Определение. Пусть Отображение 1) 2) 3) функционал называется скалярным произведением. Пространство L, наделенное скалярным произведением, напзывается предгильбертовым. Отметим, что вместо Определение. Предгильбертово пространство Н, полное относительно нормы
называется гильбертовым. Определение. Пусть Определение. Система векторов Определение. Ортогональная система векторов Определение. Счетная ортонормированная система векторов
Определение. Система векторов Определение. Система векторов Теорема (о базисе). Для счетной ортонормированной системы 1) 2) 3) Определение. Пусть L – подпространство предгильбертова пространства Е, Определение. Пусть М – подмножество предгильбертова пространства Е. Ортогональным дополнением множества М называется множество
Теорема (о разложении). Для замкнутого подпространства Е гильбертова пространства Н имеет место равенство
Следствие. Для замкнутого подпространства Е гильбертова пространства Н имеет место равенство
5.1.1 Пусть
Таблица 5.1.1
Окончание таблицы 5.1.1
5.1.2 В гильбертовом пространстве Таблица 5.1.2
Окончание таблицы 5.1.2
5.1.3. Доказать, что в указанном нормированном пространстве
Таблица 5.1.3
5.1.4. Вычислить угол между данными векторами
Таблица 5.1.4
5.1.5. Становится ли система векторов
Таблица 5.1.5
Окончание таблицы 5.1.5
5.1.6. Для данного подмножества М гильбертова пространства
Таблица 5.1.6
Окончание таблицы 5.1.6
|

 − векторное пространство над полем К
− векторное пространство над полем К 
 ,обладающее следующими свойствами:
,обладающее следующими свойствами:

 ;
; линеен для любого у,
линеен для любого у, часто пишут.
часто пишут. 
 ,
, ), если
), если 
 называется ортогональной, если входящие в нее векторы попарно ортогональны.
называется ортогональной, если входящие в нее векторы попарно ортогональны. называется ортонормированной, если
называется ортонормированной, если  при всех
при всех  .
. называется ортонормированным базисом (о.н.б.), если каждый вектор х из L разлагается в ряд Фурье по этой системе, т. е. имеет место равенство
называется ортонормированным базисом (о.н.б.), если каждый вектор х из L разлагается в ряд Фурье по этой системе, т. е. имеет место равенство .
. называется максимальной, если из того, что
называется максимальной, если из того, что  , следует, что х =0.
, следует, что х =0. следующие утверждения равносильны:
следующие утверждения равносильны: - о. н. б.;
- о. н. б.; максимальна;
максимальна; полна.
полна. . Вектор
. Вектор  называется проекцией вектора х на подпространство L, если
называется проекцией вектора х на подпространство L, если  .
. .
. .
.
 . Проверить аксиомы скалярного произведения для функции
. Проверить аксиомы скалярного произведения для функции  (таблица 5.1.1).
(таблица 5.1.1).


















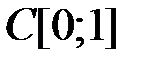

 найти проекцию вектора
найти проекцию вектора  на заданное подпространство
на заданное подпространство 









 ,
, 



 ,
, 

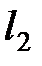

















 со стандартной нормой нельзя ввести скалярное произведение, порождающее эту норму (таблица 5.1.3).
со стандартной нормой нельзя ввести скалярное произведение, порождающее эту норму (таблица 5.1.3).









 : а) в пространстве
: а) в пространстве  , б) в пространстве
, б) в пространстве  (пространства считать вещественными) (таблица 5.1.4).
(пространства считать вещественными) (таблица 5.1.4).

















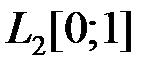








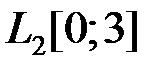









 после нормировки ортонормированным базисом пространства
после нормировки ортонормированным базисом пространства  (мы полагаем
(мы полагаем 
 единица стоит на n -ном месте) (таблица 5.1.5).
единица стоит на n -ном месте) (таблица 5.1.5).














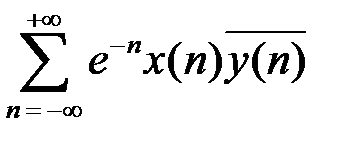







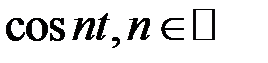

 найти ортогональное дополнение
найти ортогональное дополнение 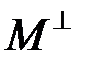 (таблица 5.1.6).
(таблица 5.1.6).

 при
при 
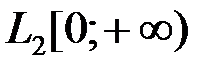

 при
при 










 при
при 

 при
при 





