1. Используя теоремы об общем виде линейных ограниченных функционалов в различных пространствах, выяснить, задает ли данная формула линейный ограниченный функционал. В случае положительного ответа найти его норму.
Пример 1. 
 ,
,  .
.
Решение. По теореме об общем виде линейного ограниченного функционала в пространстве  , для любого
, для любого 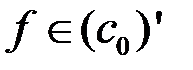 существует единственный вектор
существует единственный вектор  , такой, что для любого
, такой, что для любого 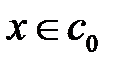 выполняется равенство
выполняется равенство 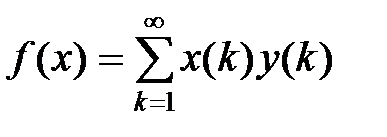 . Обратно, если выполняется это равенство, то
. Обратно, если выполняется это равенство, то 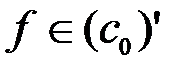 , причем
, причем 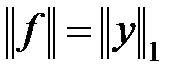 . Рассмотрим вектор
. Рассмотрим вектор 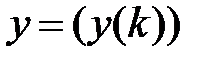 , у которого
, у которого 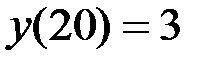 ,
,  ,
, 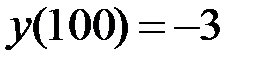 , а остальные координаты равны нулю. Тогда
, а остальные координаты равны нулю. Тогда 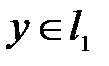 , и для этого вектора
, и для этого вектора  . В силу указанной теоремы
. В силу указанной теоремы 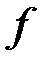 является линейным ограниченным функционалом в пространстве
является линейным ограниченным функционалом в пространстве  , и
, и
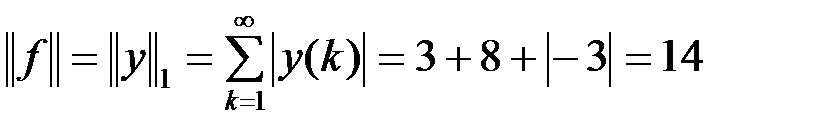 .
.
Пример 2. 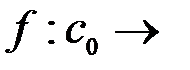
 ,
, 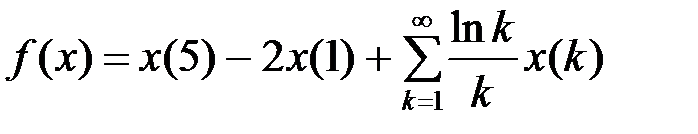 .
.
Решение. Рассмотрим вектор
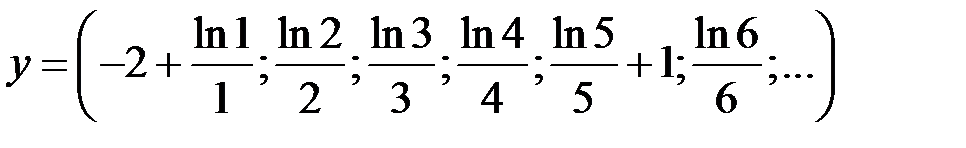 .
.
Для этого вектора выполняется равенство 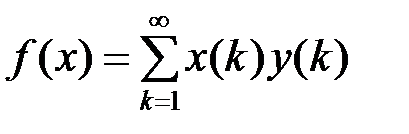 . Но
. Но 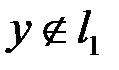 (почему?). Значит, в силу теоремы об общем виде линейного ограниченного функционала в пространстве
(почему?). Значит, в силу теоремы об общем виде линейного ограниченного функционала в пространстве  функционал
функционал 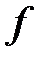 не является линейным ограниченным.
не является линейным ограниченным.
Пример 3. 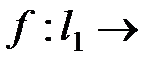
 ,
, 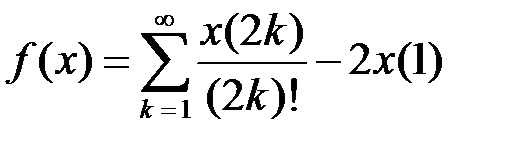 .
.
Решение. По теореме об общем виде линейного ограниченного функционала в пространстве 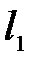 для любого
для любого 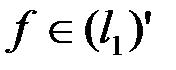 существует единственный вектор
существует единственный вектор 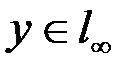 , такой, что выполняется равенство
, такой, что выполняется равенство
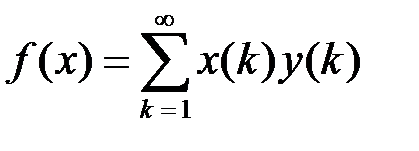 ,
,
и обратно. При этом 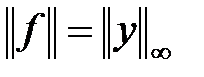 . Рассмотрим вектор
. Рассмотрим вектор  , для которого
, для которого 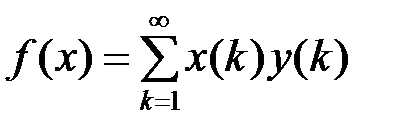 . Так как
. Так как  , то
, то 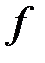 является линейным ограниченным функционалом, причем
является линейным ограниченным функционалом, причем 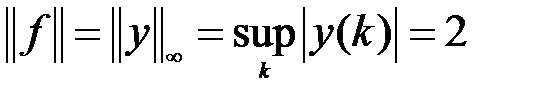 .
.
Пример 4. 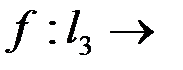
 ,
, 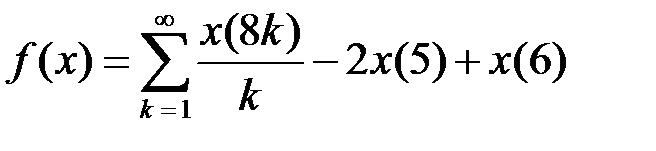 .
.
Решение. По теореме об общем виде линейного ограниченного функционала в пространстве  , для любого
, для любого 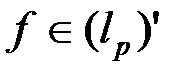 существует единственный вектор
существует единственный вектор 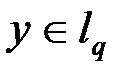
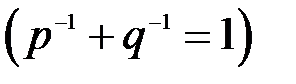 , такой, что
, такой, что  выполняется равенство
выполняется равенство 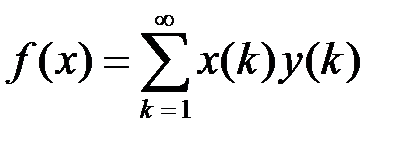 , и обратно. При этом
, и обратно. При этом  . В данном случае
. В данном случае  , а поэтому
, а поэтому 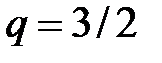 .
.
Рассмотрим вектор 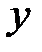 , такой, что
, такой, что 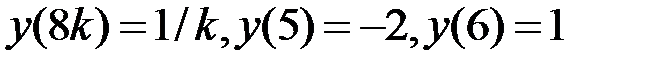 , а остальные
, а остальные 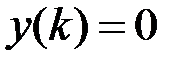 . Для этого вектора
. Для этого вектора  . Так как
. Так как 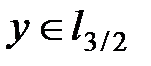 , то
, то 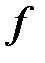 является линейным ограниченным функционалом, причем
является линейным ограниченным функционалом, причем
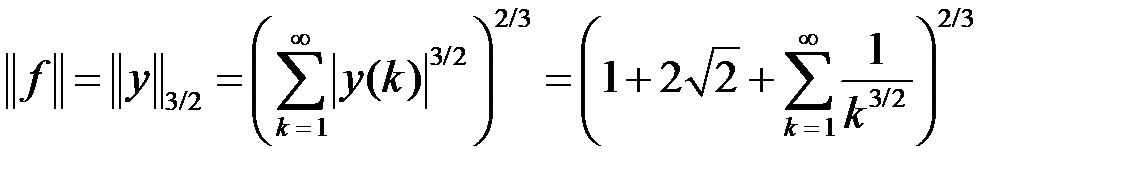 .
.
Пример 5. 
 ,
,  .
.
Решение. По теореме об общем виде линейного ограниченного функционала в пространстве 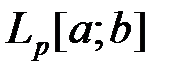 при
при  для любого
для любого 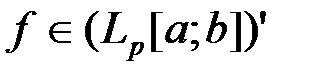 существует единственный вектор
существует единственный вектор 
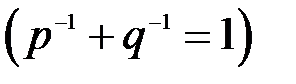 , такой, что
, такой, что 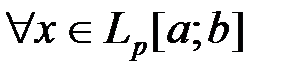 выполняется равенство
выполняется равенство  , и обратно. При этом
, и обратно. При этом  . В данном случае
. В данном случае 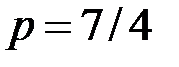 , тогда
, тогда 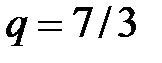 . Преобразуем интеграл
. Преобразуем интеграл
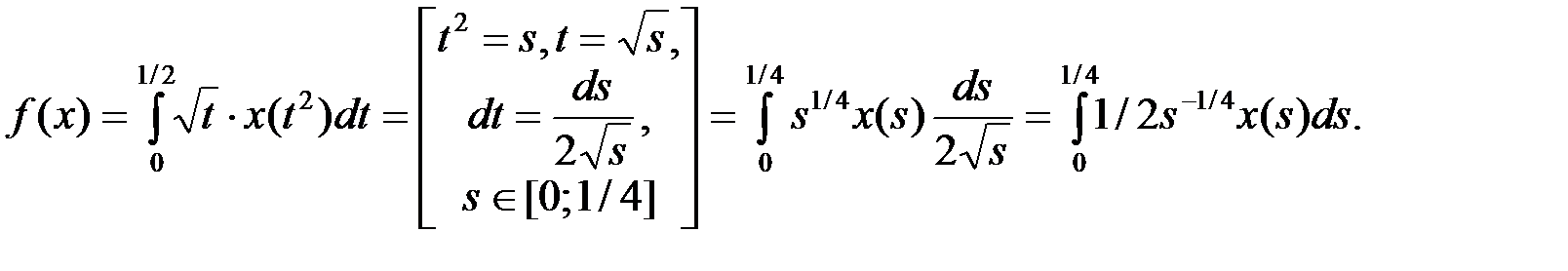
Функция
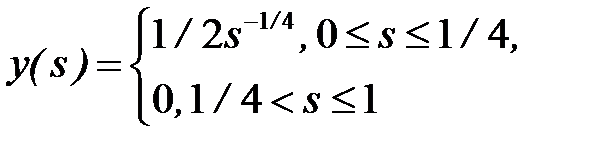
принадлежит  , так как функция
, так как функция  интегрируема по Лебегу на отрезке
интегрируема по Лебегу на отрезке 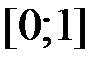 . Отсюда в силу указанной теоремы
. Отсюда в силу указанной теоремы 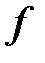 является линейным ограниченным функционалом, причем
является линейным ограниченным функционалом, причем
 .
.
Пример 6. 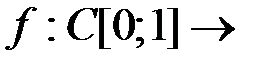
 ,
, 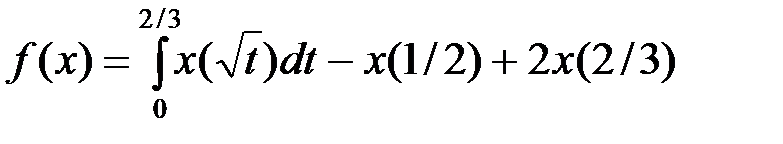 .
.
Решение. По теореме об общем виде линейного ограниченного функционала в пространстве 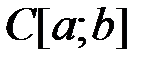 для любого
для любого 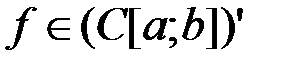 существует единственная непрерывная слева функция
существует единственная непрерывная слева функция 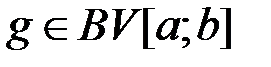 , такая, что
, такая, что 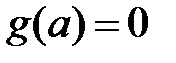 и
и 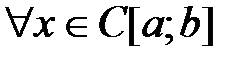 выполняется равенство
выполняется равенство 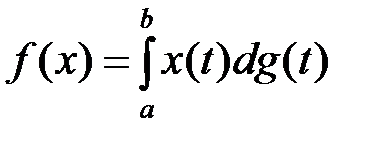 , и обратно, причем
, и обратно, причем  . Подберем функцию
. Подберем функцию  так, чтобы
так, чтобы 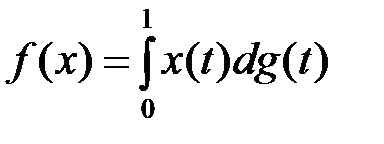
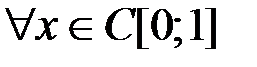 . При этом мы будем пользоваться следующей формулой:
. При этом мы будем пользоваться следующей формулой:
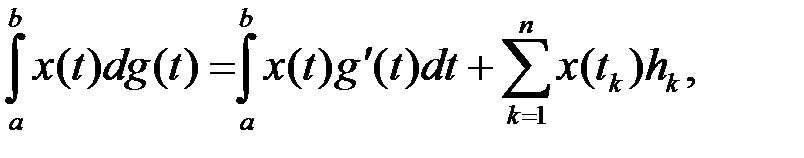 (1)
(1)
которая справедлива, если  – кусочно-непрерывно дифференцируемая функция, имеющая на
– кусочно-непрерывно дифференцируемая функция, имеющая на 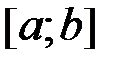 точки разрыва
точки разрыва 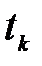 первого рода со скачками
первого рода со скачками  соответственно, а вне точек разрыва ограниченную производную. Преобразуем
соответственно, а вне точек разрыва ограниченную производную. Преобразуем  , выполнив в интеграле замену
, выполнив в интеграле замену 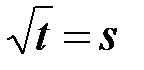 . Тогда
. Тогда
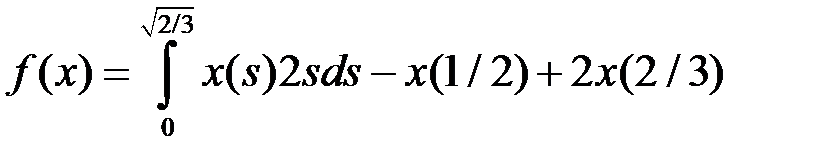 .
.
Ввиду формулы (1) отсюда следует, что 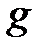 имеет 2 точки разрыва первого рода:
имеет 2 точки разрыва первого рода:  со скачком в этой точке
со скачком в этой точке 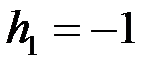 и
и 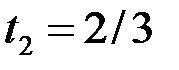 со скачком
со скачком  . При этом на интервалах непрерывности должно выполняться следующее равенство:
. При этом на интервалах непрерывности должно выполняться следующее равенство:
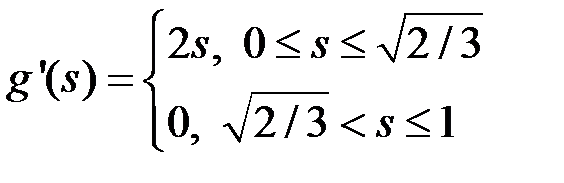 .
.
Поэтому на интервалах непрерывности, содержащихся в отрезке 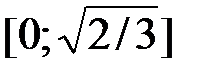 , функция
, функция 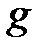 имеет вид
имеет вид  , а на интервалах непрерывности, содержащихся в отрезке
, а на интервалах непрерывности, содержащихся в отрезке 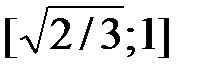 , функция
, функция 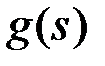 постоянна (со своей константой на каждом интервале!). Учитывая, что функция
постоянна (со своей константой на каждом интервале!). Учитывая, что функция  согласно теореме должна быть непрерывной слева на отрезке
согласно теореме должна быть непрерывной слева на отрезке 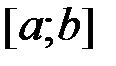 и удовлетворять условию
и удовлетворять условию 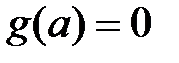 , получим (рисунок 7):
, получим (рисунок 7):
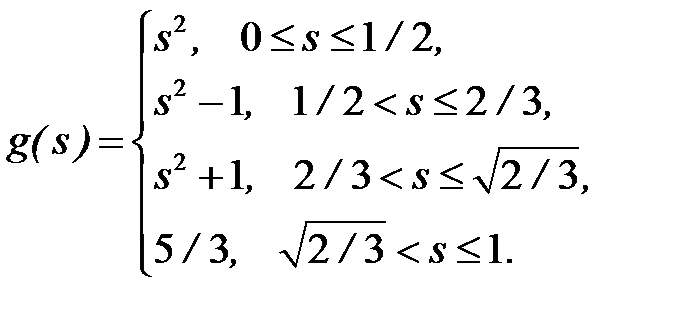
Так как
 ,
,
то  . Значит,
. Значит,  является линейным ограниченным функционалом, причем
является линейным ограниченным функционалом, причем  .
.
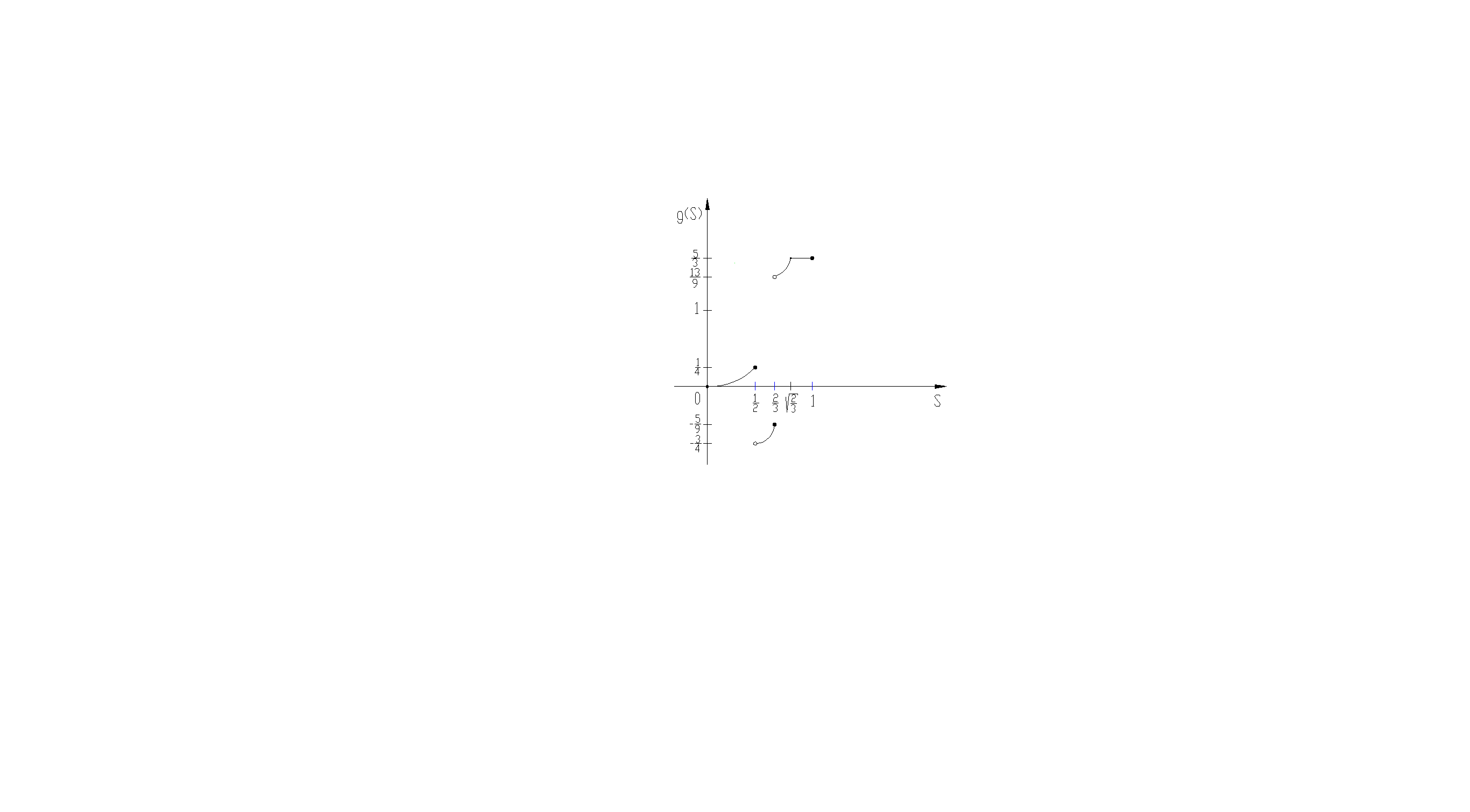
Рисунок 7 – График функции 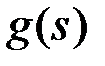
2. Пусть Х – банахово пространство над полем К. Задает ли данная формула линейный ограниченный функционал  ? В случае положительного ответа найти его норму.
? В случае положительного ответа найти его норму.
Пример 1. 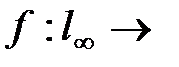
 ,
, 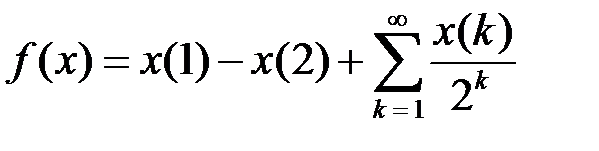 .
.
Решение. Очевидно, что функционал 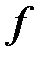 линеен. Оценим
линеен. Оценим 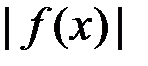 сверху:
сверху:
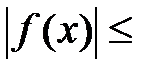
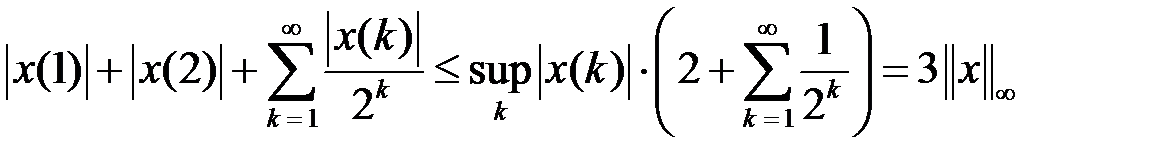 , (2)
, (2)
т. е. число 3 является константой ограниченности для 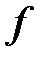 . Значит,
. Значит, 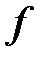 − ограниченный линейный функционал, причем
− ограниченный линейный функционал, причем
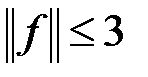 . (3)
. (3)
Подберем ненулевой вектор 
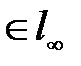 так, чтобы неравенства (2) обратились в равенства. Подходит
так, чтобы неравенства (2) обратились в равенства. Подходит  . Имеем
. Имеем 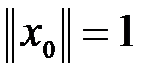 ,
,  . Следовательно,
. Следовательно,
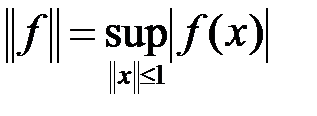
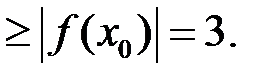 (4)
(4)
Из (3) и (4) заключаем, что  .
.
Пример 2. 
 ,
,  .
.
Решение. Очевидно, что  − линейный функционал. Так как
− линейный функционал. Так как
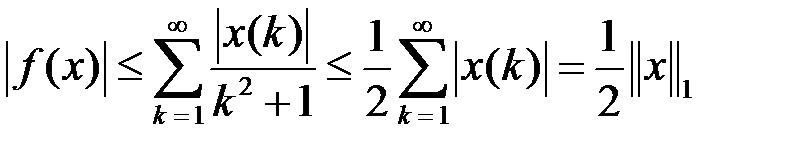 ,
,
то  ограничен, причем (см. пример 1)
ограничен, причем (см. пример 1)
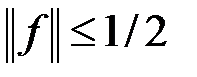 . (5)
. (5)
Возьмем 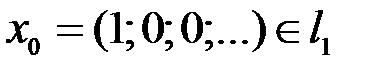 . Имеем
. Имеем 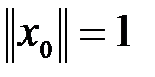 ,
, 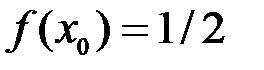 . Значит (см. пример 1),
. Значит (см. пример 1),
 . (6)
. (6)
Из неравенств (5) и (6) получаем 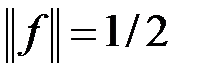 .
.
Пример 3. 
 ,
, 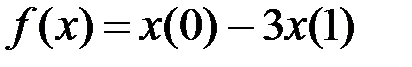 .
.
Решение. Очевидно, 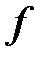 − линейный функционал. Так как
− линейный функционал. Так как
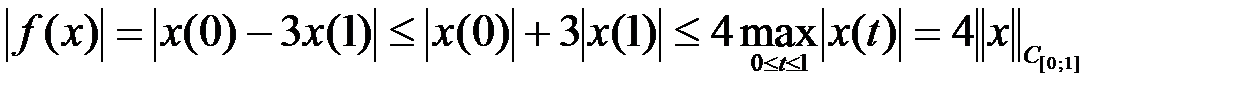 , (7)
, (7)
то  ограничен, причем (см. пример 1)
ограничен, причем (см. пример 1)
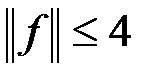 . (8)
. (8)
Подберем теперь непрерывную функцию 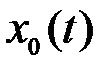 так, чтобы выполнялись следующие условия, гарантирующие, что все неравенства в (7) обращаются в равенства:
так, чтобы выполнялись следующие условия, гарантирующие, что все неравенства в (7) обращаются в равенства:
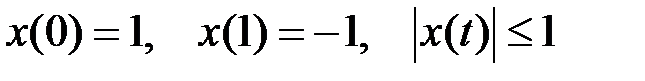 .
.
Например,  . Для нее
. Для нее 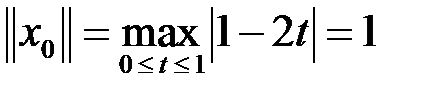 ,
, 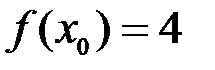 . Тогда имеем (см. пример 1)
. Тогда имеем (см. пример 1)
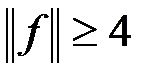 . (9)
. (9)
Вследствие неравенств (8) и (9) получаем 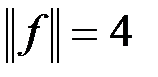 .
.


 ,
,  .
. , для любого
, для любого 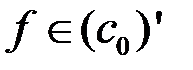 существует единственный вектор
существует единственный вектор  , такой, что для любого
, такой, что для любого 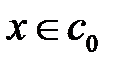 выполняется равенство
выполняется равенство 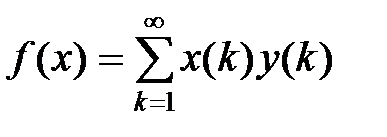 . Обратно, если выполняется это равенство, то
. Обратно, если выполняется это равенство, то 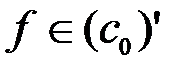 , причем
, причем 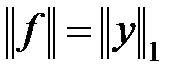 . Рассмотрим вектор
. Рассмотрим вектор 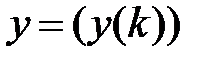 , у которого
, у которого 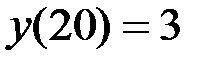 ,
,  ,
, 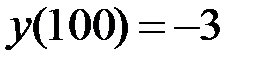 , а остальные координаты равны нулю. Тогда
, а остальные координаты равны нулю. Тогда 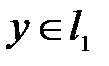 , и для этого вектора
, и для этого вектора  . В силу указанной теоремы
. В силу указанной теоремы 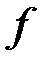 является линейным ограниченным функционалом в пространстве
является линейным ограниченным функционалом в пространстве  , и
, и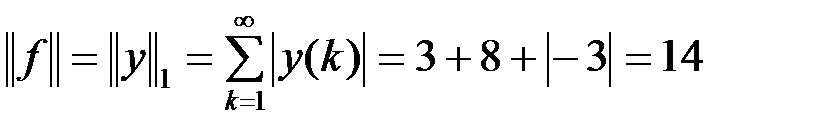 .
.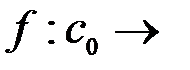
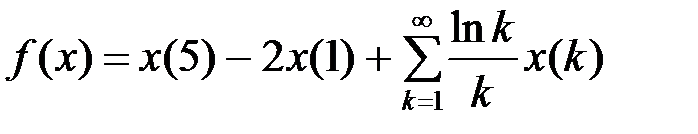 .
.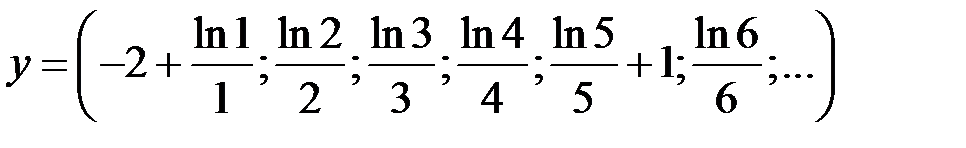 .
.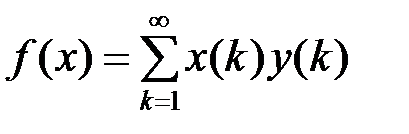 . Но
. Но 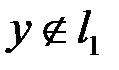 (почему?). Значит, в силу теоремы об общем виде линейного ограниченного функционала в пространстве
(почему?). Значит, в силу теоремы об общем виде линейного ограниченного функционала в пространстве  функционал
функционал 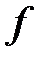 не является линейным ограниченным.
не является линейным ограниченным.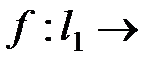
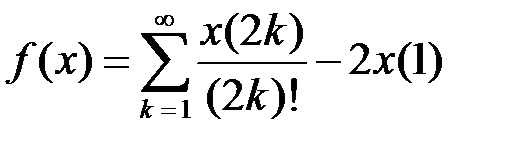 .
.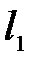 для любого
для любого 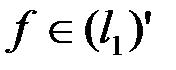 существует единственный вектор
существует единственный вектор 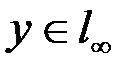 , такой, что выполняется равенство
, такой, что выполняется равенство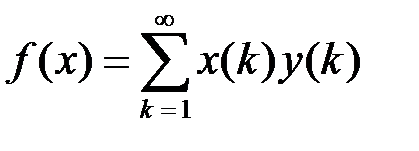 ,
,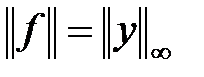 . Рассмотрим вектор
. Рассмотрим вектор  , для которого
, для которого 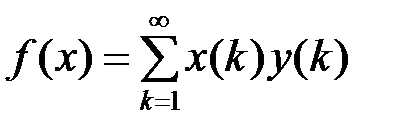 . Так как
. Так как  , то
, то 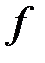 является линейным ограниченным функционалом, причем
является линейным ограниченным функционалом, причем 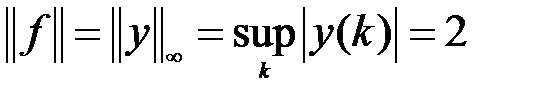 .
.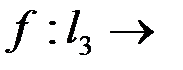
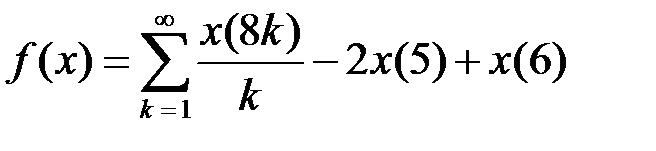 .
. , для любого
, для любого 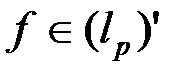 существует единственный вектор
существует единственный вектор 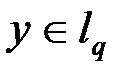
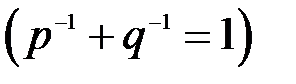 , такой, что
, такой, что  выполняется равенство
выполняется равенство 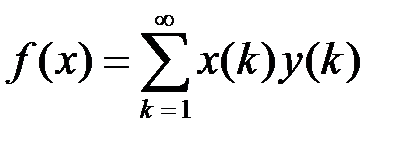 , и обратно. При этом
, и обратно. При этом  . В данном случае
. В данном случае  , а поэтому
, а поэтому 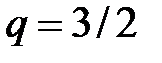 .
.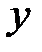 , такой, что
, такой, что 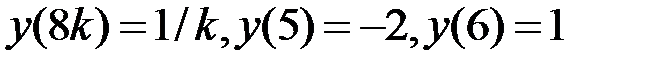 , а остальные
, а остальные 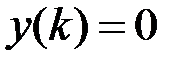 . Для этого вектора
. Для этого вектора  . Так как
. Так как 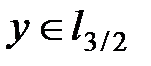 , то
, то 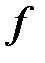 является линейным ограниченным функционалом, причем
является линейным ограниченным функционалом, причем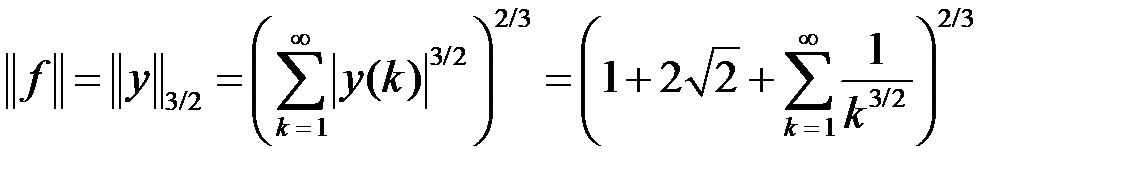 .
.
 .
.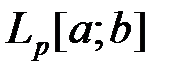 при
при  для любого
для любого 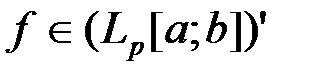 существует единственный вектор
существует единственный вектор 
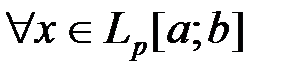 выполняется равенство
выполняется равенство  , и обратно. При этом
, и обратно. При этом  . В данном случае
. В данном случае 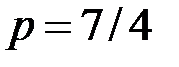 , тогда
, тогда 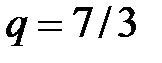 . Преобразуем интеграл
. Преобразуем интеграл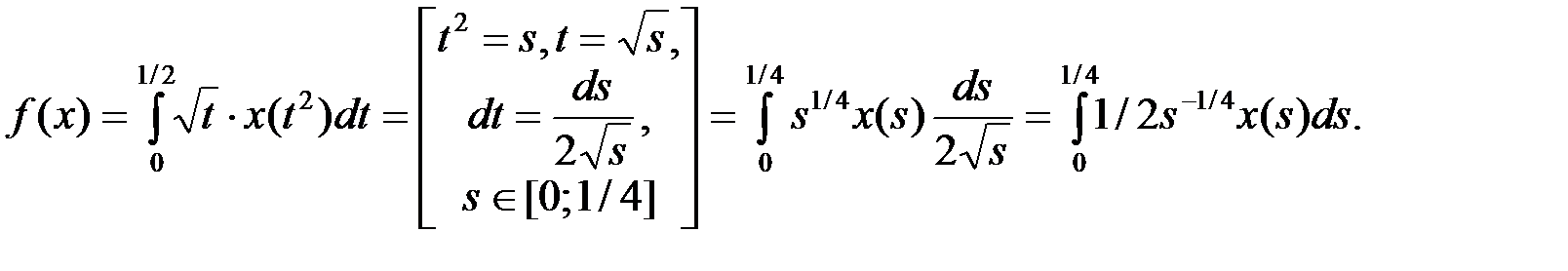
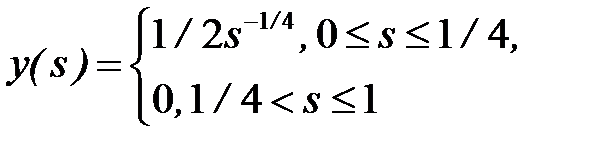
 , так как функция
, так как функция  интегрируема по Лебегу на отрезке
интегрируема по Лебегу на отрезке  . Отсюда в силу указанной теоремы
. Отсюда в силу указанной теоремы  является линейным ограниченным функционалом, причем
является линейным ограниченным функционалом, причем .
.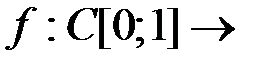
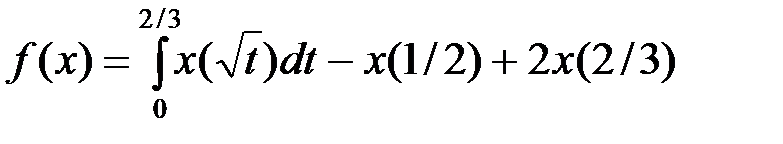 .
.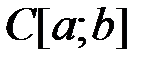 для любого
для любого 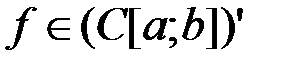 существует единственная непрерывная слева функция
существует единственная непрерывная слева функция 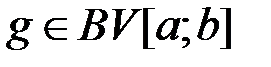 , такая, что
, такая, что 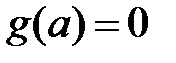 и
и 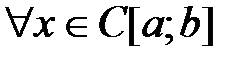 выполняется равенство
выполняется равенство 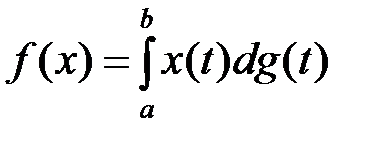 , и обратно, причем
, и обратно, причем  . Подберем функцию
. Подберем функцию  так, чтобы
так, чтобы 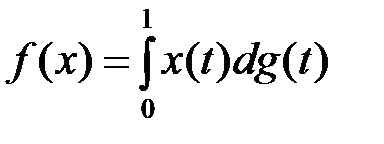
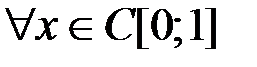 . При этом мы будем пользоваться следующей формулой:
. При этом мы будем пользоваться следующей формулой: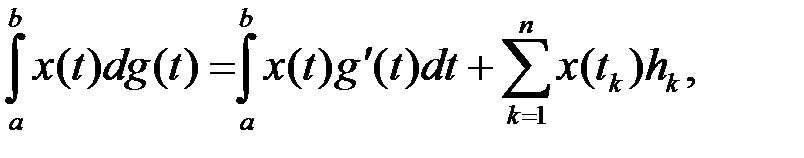 (1)
(1)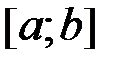 точки разрыва
точки разрыва 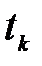 первого рода со скачками
первого рода со скачками  соответственно, а вне точек разрыва ограниченную производную. Преобразуем
соответственно, а вне точек разрыва ограниченную производную. Преобразуем  , выполнив в интеграле замену
, выполнив в интеграле замену 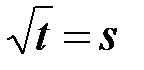 . Тогда
. Тогда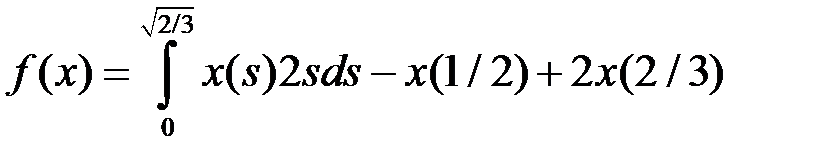 .
. имеет 2 точки разрыва первого рода:
имеет 2 точки разрыва первого рода:  со скачком в этой точке
со скачком в этой точке 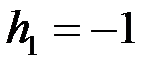 и
и 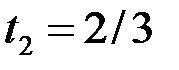 со скачком
со скачком  . При этом на интервалах непрерывности должно выполняться следующее равенство:
. При этом на интервалах непрерывности должно выполняться следующее равенство: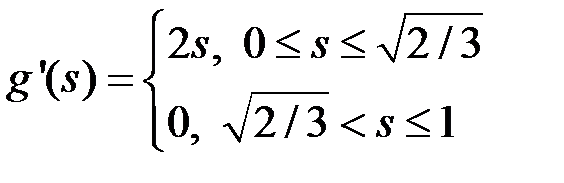 .
.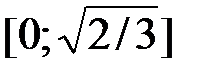 , функция
, функция 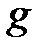 имеет вид
имеет вид  , а на интервалах непрерывности, содержащихся в отрезке
, а на интервалах непрерывности, содержащихся в отрезке 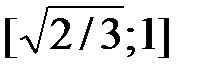 , функция
, функция 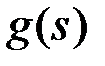 постоянна (со своей константой на каждом интервале!). Учитывая, что функция
постоянна (со своей константой на каждом интервале!). Учитывая, что функция 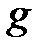 согласно теореме должна быть непрерывной слева на отрезке
согласно теореме должна быть непрерывной слева на отрезке 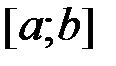 и удовлетворять условию
и удовлетворять условию 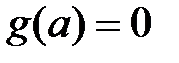 , получим (рисунок 7):
, получим (рисунок 7):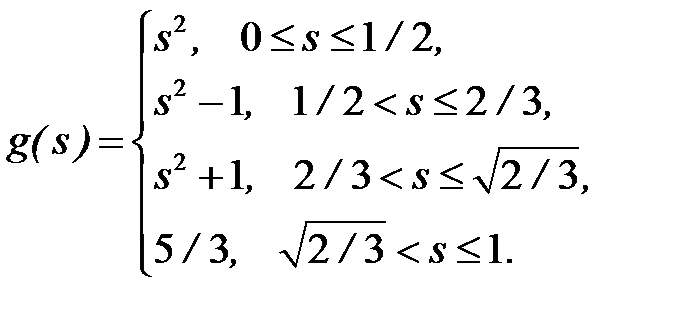
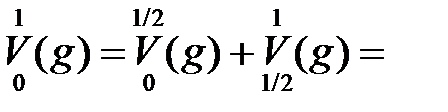
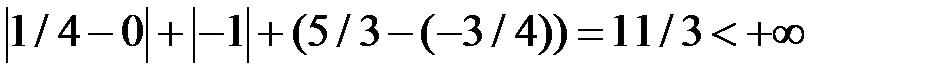 ,
, . Значит,
. Значит,  является линейным ограниченным функционалом, причем
является линейным ограниченным функционалом, причем  .
.
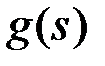
 ? В случае положительного ответа найти его норму.
? В случае положительного ответа найти его норму.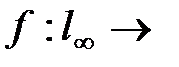
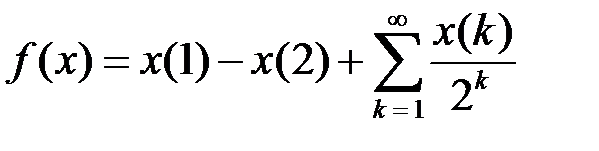 .
.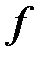 линеен. Оценим
линеен. Оценим 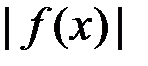 сверху:
сверху: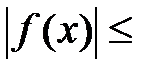
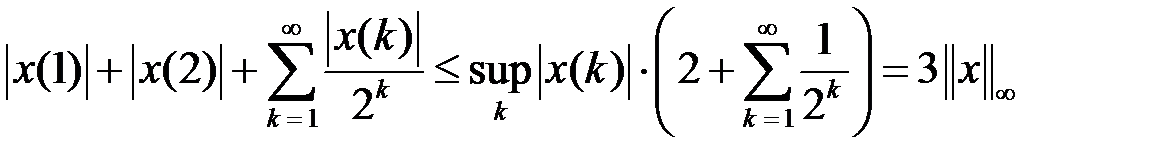 , (2)
, (2)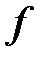 . Значит,
. Значит, 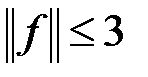 . (3)
. (3)
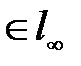 так, чтобы неравенства (2) обратились в равенства. Подходит
так, чтобы неравенства (2) обратились в равенства. Подходит  . Имеем
. Имеем 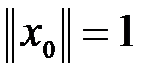 ,
,  . Следовательно,
. Следовательно,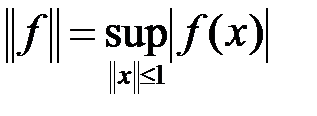
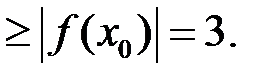 (4)
(4) .
.
 .
. − линейный функционал. Так как
− линейный функционал. Так как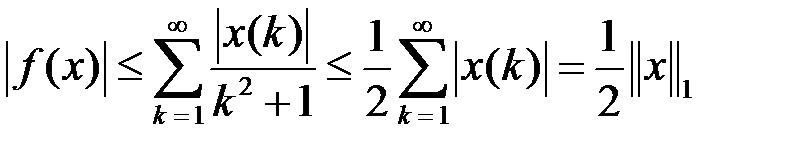 ,
, ограничен, причем (см. пример 1)
ограничен, причем (см. пример 1)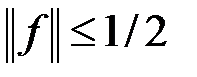 . (5)
. (5)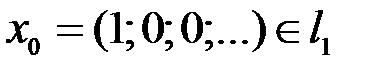 . Имеем
. Имеем 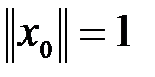 ,
, 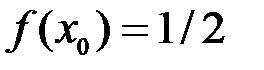 . Значит (см. пример 1),
. Значит (см. пример 1), . (6)
. (6)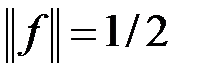 .
.
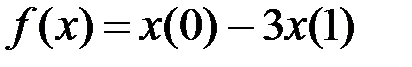 .
.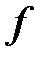 − линейный функционал. Так как
− линейный функционал. Так как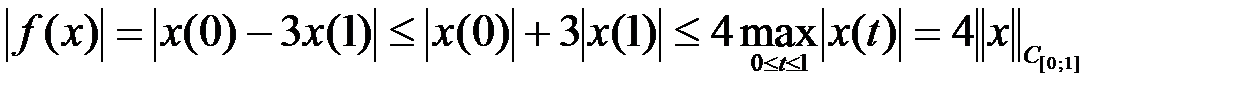 , (7)
, (7) ограничен, причем (см. пример 1)
ограничен, причем (см. пример 1)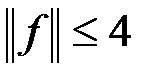 . (8)
. (8)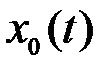 так, чтобы выполнялись следующие условия, гарантирующие, что все неравенства в (7) обращаются в равенства:
так, чтобы выполнялись следующие условия, гарантирующие, что все неравенства в (7) обращаются в равенства: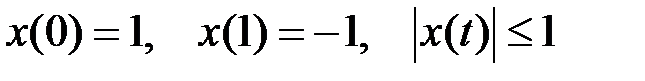 .
. . Для нее
. Для нее 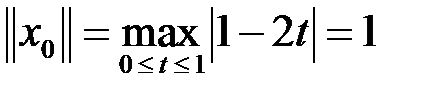 ,
, 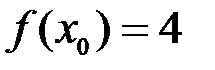 . Тогда имеем (см. пример 1)
. Тогда имеем (см. пример 1)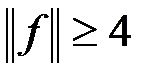 . (9)
. (9)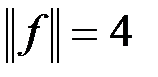 .
.


