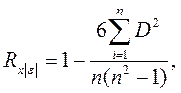Тест ранговой корреляции Спирмена

Дисперсия случайного члена уравнения регрессии в каждом наблюдении должна быть постоянной.

Под понятием дисперсия имеется ввиду возможное поведение случайного члена уравнения регрессии до того как сделана выборка.

В том случае, когда дисперсия каждого отклонения ε_i неодинакова для всех значений X_i, имеет место гетероскедастичность.

Часто появление проблемы гетероскедастичности можно предвидеть заранее, основываясь на знании характера данных. В таких случаях можно предпринять соответствующие действия по устранению этого эффекта на этапе спецификации модели регрессии. Это позволит уменьшить или возможно устранить необходимость формальной проверки.

В настоящее время существует достаточно большое число тестов для обнаружения гетероскедастичности, в которых делаются различные предположения о зависимости между дисперсией случайного члена уравнения регрессии и величиной объясняющей переменной.

При выполнении теста ранговой корреляции Спирмена предполагается, что дисперсия случайного члена уравнения регрессии будет либо увеличиваться, либо уменьшаться по мере увеличения X. И поэтому в регрессии, оцениваемой с помощью метода наименьших квадратов, абсолютные величины остатков и значения X будут коррелированны.

Данные по X и остатки (ε_i) упорядочиваются по возрастанию. Затем находится ранг для каждого значения X и ε_i.

Коэффициент ранговой корреляции определяют по формуле:

 

где:

n - количество наблюдений;

D - разность рангов X и модуля остатков D.

Если предположить, что коэффициент корреляции для генеральной совокупности равен нулю, то коэффициент ранговой корреляции имеет нормальное распределение с математическим ожиданием равным нулю:

и дисперсией:

в больших выборках.

Следовательно, соответствующая тестовая статистика равна:

И при использовании двухстороннего критерия нулевая гипотеза об отсутствии гетероскедастичности будет отклонена для генеральной совокупности при уровне значимости в 5%, если она превысит значение 1,96.

При проверке наличия или отсутствия гетероскедастичности в исследуемой модели, с помощью теста ранговой корреляции Спирмена, получаем:

 

ДЛЯ ФУНКЦИИ ПОТРЕБЛЕНИЯ: ДЛЯ ФУНКЦИИ ИНВЕСТИЦИЙ:

0,03, t_pacч = 0,16, t_кр = 1,96. 0,12, t_pacч = 0,60, t_кр = 1,96.

 

Следовательно, нулевая гипотеза принимается в обоих случаях.