КОСВЕННЫЙ МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
Для определения неизвестных параметров непосредственно из системы уравнений (1) нельзя использовать обычный метод наименьших квадратов. Это вызвано тем, что переменная Y(t) имеет корреляционную связь со случайными составляющими u1(t) и u2(t), а значит получаемые оценки параметров будут смещёнными. С целью устранения этого препятствия используем косвенный метод наименьших квадратов (КМНК). Для реализации данного метода подставим из третьего уравнения системы значение Y(t) в первое и второе уравнения системы. В результате преобразований получаем следующие уравнения:
Систему уравнений (3) можно записать в следующем виде:
где:
Для того чтобы получить из (4) систему приведённых уравнений, достаточно из второго уравнения значение переменной I(t) подставить в первое уравнение, а значение переменной C(t) из первого уравнения подставить во второе уравнение. В результате несложных преобразований имеем:
Данную систему уравнений представим в следующем виде:
где:
Система уравнений (7) является системой приведённых уравнений. В ней эндогенные переменные C(t) и I(t) выражены только через экзогенную переменную G(t) и случайные составляющие Для этого используем имеющийся в табличном редакторе Excel пакет прикладных программ, реализующий определение параметров уравнения регрессии методом наименьших квадратов. Активация этого метода осуществляется командами: «Сервис» - «Анализ данных» - «Регрессия».
Таблица №1
|

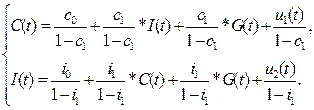 (3)
(3) (4)
(4)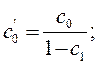

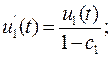 (5)
(5)

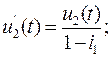 (5а)
(5а) (6)
(6)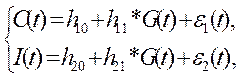 (7)
(7)
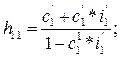
 (8)
(8)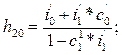
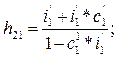
 (8а)
(8а)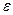 (t),
(t), 


