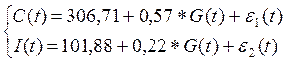Исходные данные.
| t
| G(t)
| C(t)
| I(t)
| Y(t)
| |
|
|
|
|
| |
|
|
|
|
| |
|
| 371,8
| 133,6
| 638,4
| |
|
| 407,6
| 128,2
| 691,8
| |
|
| 386,6
| 135,2
| 682,8
| |
|
| 392,4
| 137,8
| 694,2
| |
|
| 406,6
| 143,2
| 720,8
| |
|
|
|
|
| |
|
| 419,2
| 135,4
| 726,6
| |
|
| 414,8
| 138,6
| 731,4
| |
|
| 393,2
| 143,4
| 718,6
| |
|
|
|
|
| |
|
| 420,8
| 140,6
| 749,4
| |
|
|
|
|
| |
|
| 412,6
| 147,2
| 750,8
| |
|
| 406,8
| 148,6
| 753,4
| |
|
|
|
|
| |
|
| 438,8
| 144,6
| 801,4
| |
|
|
|
|
| |
|
|
|
|
| |
|
| 437,6
| 154,2
| 837,8
| |
|
|
|
|
| |
|
| 471,6
| 156,2
| 893,8
| |
|
|
|
|
|
Определение параметров уравнения регрессии приведенной формы
Используя исходную информацию и систему уравнений (7), определяем с помощью МНК значения величин h10, h11, h20, h21. Для расчетов применим табличный редактор Excel.
Построение уравнения регрессии для функции потребления
Произведем построение уравнения регрессии. Определяем сначала значения величин h10, h11. Для построения статистической модели, характеризующей значимость и точность найденного уравнения регрессии, используем табличный процессор «Excel», применив команды «Сервис» - «Анализ данных» - «Регрессия».
В диалоговом окне «Регрессия» в поле «Входной интервал Y» вводим данные по С(t), включая название реквизита. В поле «Входной интервал Х» вводим данные по G(t). Затем устанавливаем флажки в окнах «Метки» и «Уровень надежности». Установим переключатель «Новый рабочий лист» и поставим флажок в окошке «Остатки». После всех вышеперечисленных действий нажимаем кнопку «ОК» в диалоговом окне «Регрессия». Получаем следующие таблицы:
Таблица №2
| Регрессионная статистика
| | Множественный R
| 0,92
| | R-квадрат
| 0,85
| | Нормированный R-квадрат
| 0,84
| | Стандартная ошибка
| 10,07
| | Наблюдения
|
|
Таблица №3
| Дисперсионный анализ
| | | df
| SS
| MS
| F
| Значимость F
| | Регрессия
|
| 12621,37
| 12621,37
| 124,39
| 1,6E-10
| | Остаток
|
| 2232,21
| 101,46
|
|
| | Итого
|
| 14853,59
|
|
|
|
Таблица №4
| | Коэффициенты
| Стандартная ошибка
| t-статистика
| P-Значение
| Нижние 95%
| Верхние 95%
| Нижние 95,0%
| Верхние 95,0%
| | Y-пересечение
| 306,71
| 9,99
| 30,71
| 1,47E-19
| 285,99
| 327,42
| 285,99
| 327,42
| | G(t)
| 0,57
| 0,05
| 11,15
| 1,6E-10
| 0,46
| 0,67
| 0,46
| 0,67
| Таблица №5
| ВЫВОД ОСТАТКА
| |
|
|
| | Наблюдение
| Предсказанное C(t)
| Остатки
| |
| 371,71
| 7,29
| |
| 388,67
| 4,33
| |
| 381,88
| -10,08
| |
| 394,88
| 12,72
| |
| 397,71
| -11,11
| |
| 399,40
| -7,00
| |
| 403,36
| 3,24
| |
| 402,80
| -8,80
| |
| 403,93
| 15,27
| |
| 407,32
| 7,48
| |
| 409,58
| -16,38
| |
| 408,45
| -4,45
| |
| 412,97
| 7,83
| |
| 414,10
| 9,90
| |
| 414,67
| -2,07
| |
| 418,62
| -11,82
| |
| 428,23
| -3,23
| |
| 429,93
| 8,87
| |
| 433,88
| 5,12
| |
| 442,36
| -16,36
| |
| 445,75
| -8,15
| |
| 450,84
| 8,16
| |
| 457,06
| 14,54
| |
| 459,32
| -5,32
|
Получаем уравнение регрессии: C(t) = 306,71+ 0,57*G(t) + e1 (t)
h10 =306,71; h11 =0,57.
Построение уравнения регрессии для функции инвестиций
Используя исходную информацию по I(t) и по G(t), систему уравнений (7), определяем с помощью МНК значения величин h20, h21. Для расчетов снова применим табличный редактор Excel (программа «Регрессия»).
Таблица №6
| Регрессионная статистика
| | Множественный R
| 0,91
| | R-квадрат
| 0,83
| | Нормированный R-квадрат
| 0,82
| | Стандартная ошибка
| 4,19
| | Наблюдения
|
| Таблица №7
Дисперсионный анализ
| | df
| SS
| MS
| F
| Значимость F
| | Регрессия
|
| 1838,75
| 1838,75
| 104,79
| 7,88E-10
| | Остаток
|
| 386,05
| 17,55
|
|
| | Итого
|
| 2224,80
|
|
|
|
Таблица №8
| | Коэффициенты
| Стандартная ошибка
| t-статистика
| P-Значение
| Нижние 95%
| Верхние 95%
| Нижние 95,0%
| Верхние 95,0%
| | Y-пересечение
| 101,88
| 4,15
| 24,53
| 1,8E-17
| 93,27
| 110,50
| 93,27
| 110,50
| | G(t)
| 0,22
| 0,02
| 10,24
| 7,88E-10
| 0,17
| 0,26
| 0,17
| 0,26
| Таблица №9
Вывод остатка
| Наблюдение
| Предсказанное I(t)
| Остатки
| |
| 126,69
| -4,69
| |
| 133,16
| 4,84
| |
| 130,57
| 3,03
| |
| 135,54
| -7,34
| |
| 136,62
| -1,42
| |
| 137,26
| 0,54
| |
| 138,77
| 4,43
| |
| 138,56
| 2,44
| |
| 138,99
| -3,59
| |
| 140,28
| -1,68
| |
| 141,15
| 2,25
| |
| 140,71
| 4,29
| |
| 142,44
| -1,84
| |
| 142,87
| -3,87
| |
| 143,09
| 4,11
| |
| 144,60
| 4,00
| |
| 148,26
| -4,26
| |
| 148,91
| -4,31
| |
| 150,42
| 3,58
| |
| 153,66
| 5,34
| |
| 154,95
| -0,75
| |
| 156,89
| -6,89
| |
| 159,27
| -3,07
| |
| 160,13
| 4,87
| |
|
|
| Получаем уравнение регрессии: I(t)=101,88+0,22*G(t)+ e2 (t)
h20 =101,88; h21 =0,22
Вывод:
Исходя из полученных значений
| h10
| 306.71
| | h11
| 0.57
| | h20
| 101.88
| | h21
| 0.22
|
получаем следующую систему приведенных уравнений:
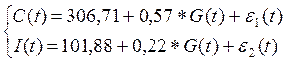

Кардиналистский и ординалистский подходы Кардиналистский (количественный подход) к анализу полезности основан на представлении о возможности измерения различных благ в условных единицах полезности...
|

Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями...
|

Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм...
|

Важнейшие способы обработки и анализа рядов динамики Не во всех случаях эмпирические данные рядов динамики позволяют определить тенденцию изменения явления во времени...
|
Приложение Г: Особенности заполнение справки формы ву-45
После выполнения полного опробования тормозов, а так же после сокращенного, если предварительно на станции было произведено полное опробование тормозов состава от стационарной установки с автоматической регистрацией параметров или без...
Измерение следующих дефектов: ползун, выщербина, неравномерный прокат, равномерный прокат, кольцевая выработка, откол обода колеса, тонкий гребень, протёртость средней части оси
Величину проката определяют с помощью вертикального движка 2 сухаря 3 шаблона 1 по кругу катания...
Неисправности автосцепки, с которыми запрещается постановка вагонов в поезд. Причины саморасцепов ЗАПРЕЩАЕТСЯ: постановка в поезда и следование в них вагонов, у которых автосцепное устройство имеет хотя бы одну из следующих неисправностей:
- трещину в корпусе автосцепки, излом деталей механизма...
|
Эндоскопическая диагностика язвенной болезни желудка, гастрита, опухоли Хронический гастрит - понятие клинико-анатомическое, характеризующееся определенными патоморфологическими изменениями слизистой оболочки желудка - неспецифическим воспалительным процессом...
Признаки классификации безопасности Можно выделить следующие признаки классификации безопасности.
1. По признаку масштабности принято различать следующие относительно самостоятельные геополитические уровни и виды безопасности.
1.1. Международная безопасность (глобальная и...
Прием и регистрация больных Пути госпитализации больных в стационар могут быть различны. В центральное приемное отделение больные могут быть доставлены:
1) машиной скорой медицинской помощи в случае возникновения острого или обострения хронического заболевания...
|
|