ПОСЛЕДОВАТЕЛЬНОСТЬ ПРОВЕРОЧНОГО РАСЧЕТА ВАЛОВ НА УСТАЛОСТНУЮ И СТАТИЧЕСКУЮ ПРОЧНОСТЬ
(см. решение примера. 41) Исходные данные: 1. Нагрузка на вал. 2. Условия работы. 3. Чертеж узла. Последовательность расчета: 1. По чертежу узла составляют расчетную схему. 2. Определяют силы, действующие на вал. 3. Строят эпюры изгибающих моментов в двух взаимно перпендикулярных плоскостях. 4. Строят эпюру крутящих моментов,
5. В соответствии с формой вала и эпюрами моментов выявляют предположительно опасные сечения, подлежащие проверке на усталостную прочность. 6. Для каждого из указанных сечений по формуле (11.2) определяют расчетные коэффициенты запаса прочности n и сравнивают с допускаемым значением [n]. При этом должно соблюдаться условие n>=[n]. 7. Если вал в период работы испытывает кратковременные перегрузки, то наиболее нагруженные сечения его проверяют на статическую прочность по формуле (11.5). В зависимости от результатов проверочного расчета конструкцию вала оставляют без изменения или в нее вносят исправления. В последнем случае проверочный расчет повторяют. Пример 41. По данным примера 40 проверить вал редуктора на усталостную и статическую прочность (см. рис. 4.2 и 11.9, а). Диаметр делительной окружности зубчатого колеса d д2= 256 мм. Сила давления цепи на вал Q=2713н и направлена под углом θ=30о к горизонту. Нагрузка на вал нереверсивная, постоянная. Работа спокойная. В период пуска кратковременная (пиковая) нагрузка в 1,8 раза больше номинальной. Зубчатое колесо вращается по часовой стрелке, если смотреть на него со стороны звездочки. (Начало расчета см. в решениях примеров 10; 18; 38; 39 и 40.) Решение. 1. Составляем расчетную схему вала (рис. 11.9, б) в соответствии с конструкцией, принятой в примере 40. 2. Определяем силы, действующие на вал (см. рис. 11.9, б). Окружное усилие на колесе P=2М/d д2 =2·189,5·103/256=1486 н. Радиальное усилие на колесе (формула 6.32) T = P·tg α=1486·tg 20о=540 н. Силу давления цепи на вал Q раскладываем на составляющие в вертикальной и горизонтальной плоскостях: Qв = Q sin θ = 2713 sin 30о = 1357 н, Qг = Q cos θ =2713 cos 30о = 2352 н.
Рис. 11.9. К расчету вала
3. Строим эпюры изгибающих моментов. В вертикальной плоскости (рис. 11.9, в): а) Определяем опорные реакции ΣМБ =0; - QВ · 70 - Р·60 + RГв ·120 = 0; RГв = (QВ·70 + Р·60)/120 = (1357·70 + 1486·60)/120 = 1534 н; ΣМГ =0; - QВ · 190 + Р·60 + RБв ·120 = 0; RБв = (QВ·190 - Р·60)/120 = (1357·190 - 1486·60)/120 = 1405 н. б) Проверяем правильность определения реакций: ΣY = Qв - RБв - Р+ RГв = 1357 - 1405 – 1486 + 1534 = 0 — реакции найдены правильно. в) Строим эпюру изгибающих моментов Мив, для чего определяем их значения в характерных сечениях вала: в сечении А Мив = 0; в сечении Б Мив = Qв · 70 =1357·70=94,9·103 н·мм; в сечении В Мив = RГв ·60 =1534·60=92 · 103 н·мм; в сечении Г Мив = 0. В горизонтальной плоскости (рис. 11.9, г): а) Определяем опорные реакции: ΣМБ =0; - QГ · 70 + Т·60 + RГг ·120 = 0; RГг = (QГ·70 - Т·60)/120 = (2352·70 - 540·60)/120 = 1102 н; ΣМГ =0; - QГ · 190 - Т·60 + RБг ·120 = 0; RБг = (QГ·190 + Т·60)/120 = (2352·190 - 546·60)/120 = 3994 н. б) Проверяем правильность определения реакций: ΣХ = QГ - RБг + Т+ RГг = 2352 - 3994 + 540 + 1102 = 0 — реакции найдены правильно. в) Строим эпюру изгибающих моментов МИГ, для чего определяем их значения в характерных сечениях вала: в сечении А Миг = 0; в сечении Б Миг = Qг · 70 =2352·70=164,6·103 н·мм; в сечении В Миг = RГг ·60 =1102·60= 66,1 ·103 н·мм; в сечении Г Миг = 0. 4. Строим эпюру крутящих моментов (рис. 11.9, д). Передача вращающего момента происходит вдоль оси вала от середины ступицы колеса до середины ступицы звездочки (см. рис. 11.9, а) МК = М = 189,5 103 н·мм. 5. В соответствии с формой вала и эпюрами Ми и Мк предположительно опасными сечениями вала, подлежащими проверке на усталостную прочность, являются сечения I-II, II-II и III-III, в которых имеются концентраторы напряжений и возникают наибольшие моменты. 6. Определяем запас усталостной прочности в сильно нагруженном сечении II-II, в котором концентрация напряжений обусловлена канавкой с галтелью (см. рис. 11.4, а) и посадкой внутреннего кольца подшипника с натягом. Эго сечение расположено на расстоянии 15 мм от середины подшипника. а) Определяем изгибающие моменты в сечении II - II. Из рис. 11.9, в Мив II = QВ · 85- RБв · 15 = 1357· 85 - 1405· 15 = 94,2 103 н·мм. Из рис. 11.9, г Mиг II = QГ · 85 - RБг ·15 = 2352 ·85 - 3994· 15= 140 ·103 н·мм. Суммарный изгибающий момент в сечении II - II
б) Согласно эпюре крутящий момент в сечении II - II Мк = 189,5 103 н·мм. в) Определяем номинальные напряжения в сечении 11 — 11. Напряжения изгиба σи =Ми II/W= Ми II/(0,1d13)=168,6·103/(0,1·403)=26,3 н/мм2. В сечении II-II отсутствуют продольные силы, следовательно, нормальные напряжения в этом сечении изменяются по симметричному циклу с амплитудой σ а = σи = 26,3 н/мм2; σm=0. Напряжения кручения τк =Мк/Wк= Мк/(0,2d13)=189,5·103/(0,2·403)=14,8 н/мм2. При отнулевом цикле изменения касательных напряжений τ а = τm = τк/2=14,8/2=7,4 н/мм2. г) В сечении II-II два концентратора напряжений: канавка с галтелью и посадка с натягом. Согласно примечаниям к табл. 11.1 в расчет принимаем концентрацию напряжений от посадки внутреннего кольца подшипника, для которой kσ=2,4 и kτ=1,8. По табл. 11.2 εσ=0,88, ετ=0,81. д) Определяем коэффициенты запаса прочности вала в сечении II-II по нормальным и касательным напряжениям. По формуле (11.3) определяем коэффициент запаса прочности по нормальным напряжениям
По формуле (11.4) определяем коэффициент запаса прочности по касательным напряжениям
где τ-1 =0,58σ-1 =0,58·253= 147 н/мм2, ψτ=0,05 (см. выше). Расчетный коэффициент запаса прочности вала в сечении II-II (формула 11.2)
Усталостная прочность вала в сечении II — II обеспечена. 7. Проверяем статическую прочность вала в сечении II—II. а) В период пуска кратковременная (пиковая) нагрузка в 1,8 раза больше номинальной, следовательно, в сечении II—II возникают пиковые изгибающий и крутящий моменты: Ми пик II = 1,8Mи II = 1,8·168,6·103=303·103 н·мм; Мк пик II = 1,8Mк II = 1,8·189,5·103=340·103 н·мм. б) Расчетные нормальное и касательное напряжения в сечении II—II в период пуска: σмах II =Ми пикII/W= Ми пикII/(0,1d13)=303·103/(0,1·403)=47,3 н/мм2. τк II =Мк пикII /Wк= Мк пикII /(0,2d13)=340·103/(0,2·403)=26,3 н/мм2. в) Предельное допускаемое напряжение для стали 45 [σ]пред=0,8στ=0,8·294=235 н/мм2. г) По формуле (11.5) эквивалентное напряжение
Статическая прочность вала в сечении II — II обеспечена. Проверочный расчет вала на усталостную и статическую прочности в сечениях I — I и III — III предлагается студентам произвести самостоятельно. Задача 38. По данным примера 41 определить коэффициент запаса усталостной прочности вала для сечения III-III под серединой зубчатого колеса. О т в е т. nIII = 5 43. Контрольные вопросы 1. Объясните, для чего при расчете вала строят эпюры изгибающих и крутящих моментов? 2, Какие сечения вала предположительно опасны? 3. Укажите конструктивные и технологические способы повы- шения усталостной прочности валов. 4. В каких случаях вал проверяют на статическую прочность? 3АНЯТИЕ 46
|


 н·мм.
н·мм.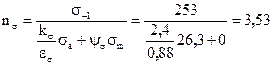 .
. ,
, .
. .
.


