Вопрос 10 Основной закон динамики вращения
Моментом силы F относительно неподвижной точки О называется физическая величина, определяемая векторным произведением радиус-вектора r, проведенного из точки О в точку А приложения силы, на силу F (рис. 1.20): М = [ rF ].
Здесь М – псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращенииот r к F. Модуль момента силы
где α – угол между r и F; r sin α= l – кратчайшее расстояние между линией действия силы и точкой О – плечо силы. Найдем выражение для работы при вращении тела (рис. 1.22). Пусть сила F приложена в точке В, находящейся от оси z на расстоянии r, α; – угол между направлением силы и радиус-вектором r. Так как тело абсолютно твердое, то работа этой силы равна работе, затраченной на поворот всего тела. При повороте тела на бесконечно малый угол dφ; точка приложения В проходит путь ds=rd φ и работа равна произведению проекции силы на направление смещения на величину смещения:
dA = F sin α r dφ;. Учитывая (1.47), можем записать dA = M z dφ; где Fr sin α=Fl=M z – момент силы относительно оси z. Таким образом, работа при вращении тела равна произведению момента действующей силы на угол поворота. Работа при вращении тела идет на увеличение его кинетической энергии: dA = dT,но
Уравнение (1.48) представляет собой уравнение динамики вращательного движения твердого тела относительно неподвижной оси.
где J – главный момент инерции тела (момент инерции относительно главной оси). Моментом импульса (количества движения) материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением:
где r – радиус-вектор, проведенный из точки О в точку A; p = m v – импульс материальной точки (рис. 1.22); L – псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от r к р. Модуль вектора момента импульса L = rp sin α = mvr sin α = pl, где α – угол между векторами r и р, l – плечо вектора p относительно точки О.
|


 -
-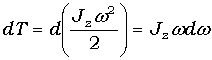 , поэтому
, поэтому  , или
, или
 Если ось z совпадает с главной осью инерции, проходящей через центр масс, то имеет место векторное равенство
Если ось z совпадает с главной осью инерции, проходящей через центр масс, то имеет место векторное равенство
 L = [ rр ] = [ r, m v ],
L = [ rр ] = [ r, m v ],


