Свойства степенных рядов
Теорема 1. Всякий степенной ряд (2) с радиусом сходимости R > 0 сходится равномерно на всяком отрезке, содержащемся в интервале сходимости (-R,R). Теорема 2. Сумма степенного ряда (2) есть ф-ция, непрерывная в каждой точке интервала сходимости ряда. Степенной ряд в его интервале сходимости можно почленно дифференцировать и интегрировать сколько угодно раз, причем в результате этих операций получаются степенные ряды, имеющие тот же радиус сходимости, что и исходный ряд. Интегрирование и дифференцирование степенных рядов позволяет заданные ряды сводить к уже известным рядам.
Пример 1. Вычислить Сопоставим заданному числовому ряду степенной ряд
Исследуем ряд на сходимость по признаку Даламбера: К какому ряду он ближе всего? К ряду геометрической прогрессии
Следовательно
Пример 2. Вычислить Сопоставим заданному числовому ряду степенной ряд
Преобразуем ряд геометрической прогрессии к заданному ряду, продифференцировав его:
|
.
.
.
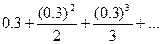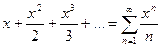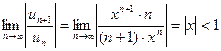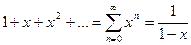, который равномерно сходится при 
Исходный ряд можно получить посредством интегрирования ряда геометрической прогрессии
.
.
.
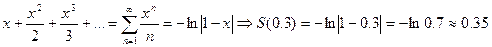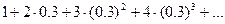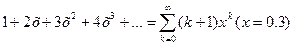. Очевидно ряд сходится при 
.
.
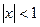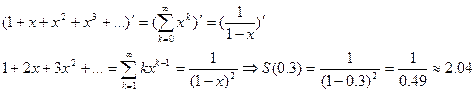