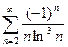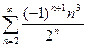Абсолютная сходимость рядов.
В этом параграфе будем изучать ряды, члены которых являются действительными числами любого знака. Опр. Ряд, члены которого имеют как положительные, так и отрицательные члены, называют знакопеременным.
Теорема. Пусть дан знакопеременный ряд
Опр. Пусть даны два ряда сходится, то ряд (1) сходится абсолютно. Если ряд (1) сходится, а ряд (2) расходится, то ряд (1) сходится условно.
Свойства абсолютно сходящихся рядов
1) Слагаемые абсолютно сходящихся рядов можно менять местами, не изменяя сумму ряда. Если ряд сходится условно, то при перемене мест его слагаемых можно получить сумму ряда, равную любому заранее заданному числу, и более того, можно получить ряд расходящийся. 2) Абсолютно сходящиеся ряды в отличие от условно сходящихся можно перемножать. При этом сумма произведения рядов будет равна произведению сумм рядов сомножителей.
Схема исследования на сходимость знакочередующихся рядов
1. Составляем ряд из абсолютных величин данного знакочередующегося ряда и ииследуем сходимость полученного знакоположительного ряда с помощью одного из достаточных признаков сходимости. Делаем вывод: если ряд из абсолютных величин сходится, то исходный знакочередующийся ряд сходится абсолютно, если расходится, то исследуем исходный ряд на условную сходимость, проверяем выполнение признака Лейбница: Если Если Замечание. Если общий член знакочередующегося ряда имеет такой вид, что легко найти
Примеры: Исследовать на абсолютную и условную сходимость ряд:
1)
2) 3) 4)
5)
6)
7)
8)
9)
|

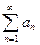 (1) и ряд, составленный из его модулей
(1) и ряд, составленный из его модулей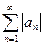 (2). Тогда, если ряд (2) сходится, то ряд (1) тоже сходится.
(2). Тогда, если ряд (2) сходится, то ряд (1) тоже сходится. , то утверждаем, что ряд расходится.
, то утверждаем, что ряд расходится.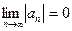 , то ряд сходится условно.
, то ряд сходится условно.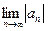 , то начинаем исследование с проверки выполнения признака Лейбница.
, то начинаем исследование с проверки выполнения признака Лейбница.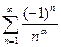 (1)
(1) 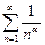 (2) Ряд (1) при α > 0 сходится по Лейбницу. Ряд (2) - эталонный ряд, сходится при α > 1. Следовательно при 0 < α
(2) Ряд (1) при α > 0 сходится по Лейбницу. Ряд (2) - эталонный ряд, сходится при α > 1. Следовательно при 0 < α 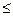 1 ряд (1) сходится условно и при α > 1 ряд сходится абсолютно.
1 ряд (1) сходится условно и при α > 1 ряд сходится абсолютно.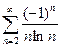 (сходится условно). 10)
(сходится условно). 10) 
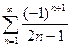 11)
11) 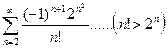
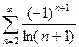 12)
12) 
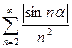 13)
13) 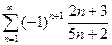
 14)
14) 
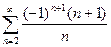 15)
15) 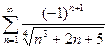
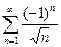 16)
16)