Необходимое условие сходимости числового ряда
Теорема. Если числовой ряд сходится .
Приведенный признак сходимости следует понимать так: Если если
Пример. Исследовать на сходимость ряды:
1.
2.
3.
4.
5. Таблица эквивалентных величин
При при
Пример. Выполняется ли необходимый признак сходимости ряда?
Факт расходимости ряда при выполнении необходимого признака сходимости говорит о том, что для сходимости ряда кроме убывания и стремления к нулю общего члена ряда нужна достаточная скорость убывания ряда, чтобы сумма бесконечного числа членов не успела накапливаться. Прежде, чем вычислять сумму ряда необходимо убедиться, что он сходится. Достаточные признаки сходимости числовых рядов дают ответ на эти вопросы.
|
, тогда предел его общего члена равен 0:
, то ряд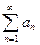 
расходится точно,
, то ряд 
, 
ряд расходится.
, 
ряд расходится.
, 
ряд расходится.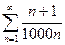
, 
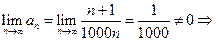ряд расходится.
, 
ряд может как сходиться, так и расходиться.
- многочлен степени n.
,
.
