Понятие числового ряда и его сходимости
Числовые ряды
Опр. Пусть задана числовая последовательность числовой последовательности Числа
Опр. Если все члены ряда аn > 0(положительны), то ряд называется знакоположительным.
Опр. Сумма первых n слагаемых ряда называется n – частичной суммой ряда:
Опр. Если предел n – частичной суммы ряда существует и конечен, то ряд называется сходящимся, в противном случае (предел n – частичной суммы ряда не существует или равен бесконечности) говорят, что ряд расходится.
Опр. Остатком ряда после n-го члена (или n-м остатком) Rn называют ряд, полученный из данного путем отбрасывания его n первых членов Тогда сумма ряда может быть записана выражением
Свойства сходящихся числовых рядов
1. Ряд и его остаток либо одновременно сходятся, либо расходятся. Остаток сходящегося ряда стремится к нулю: 2. Сходящиеся ряды можно почленно складывать, вычитать, умножать все члены сходящегося ряда на постоянное число, перемножать ряды как два многочлена, и при этом полученные ряды будут являться сходящимися, т.е если то
|
. Сумма элементов бесконечной
называется числовым рядом.
называются членами ряда, n-ый член ряда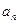 
называется общим членом ряда.
.
. Этот предел называется суммой числового ряда.
,
,
,
.
.
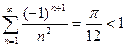. Так как сумма Sn первых n членов ряда всегда конечное число, то сходимость ряда определяется сходимостью его остатка Rn=S – Sn.
.
, 
,
, 
, 
.
