Признак сравнения 2
Пусть даны два знакоположительных ряда
Если предел отношения этих рядов существует и конечен
Замечание. При применении признака сравнения данный ряд сопоставляется с одним из эталонных рядов, сходимость и расходимость которых установлена. Эталонные ряды: 2) Геометрический ряд
2) Ряд
Суть использования признака сравнения, особенно его предельной формы, состоит в том, что нужно для данного ряда организовать эквивалентный ему ряд в виде одного из эталонных рядов и сделать вывод о его сходимости.
Пример 1. Исследовать на сходимость ряд
Ряд Очевидно
Пример 2. Исследовать на сходимость ряд Ряд Очевидно
Пример 3. Исследовать на сходимость ряд Вспомним таблицу эквивалентных б.м. величин
Признаки сравнения просты в использовании и очень эффективны, но, к сожалению, не всегда могут быть использованы. Поэтому рассмотрим другие признаки сходимости.
|
, то ряды (1) и (2) ведут себя одинаково (сходятся и расходятся одновременно).
- 
.
.
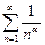(1) сравним с рядом 
(2):
для n > 2. Ряд 
сходится как геометрический ряд (q<1). Следовательно, меньший ряд (1) тем более сходится по признаку сравнения 1.
.
(2).
. Ряд (2) сходится как геометрический ряд 
(q<1). Следовательно, меньший ряд (1) тем более сходится по признаку сравнения 1.
.
. Поэтому сравним ряд 
(2). Ряд (2) сходится как геометрический ряд (q<1). Найдем 
. Следовательно оба ряда ведут себя одинаково и ряд (1) сходится по признаку сравнения 2.
