Степенные ряды
Степенные ряды – это простейшие функциональные ряды.
Опр. Степенным рядом называется ряд вида
по степеням (х –с). аn – числа, коэффициенты ряда, с – число. В простейшем случае с = 0, тогда ряд (1) приобретает вид
Очевидно, что путем подстановки
Теорема Абеля. Если степенной ряд (2) сходится при сходится для любого х, удовлетворяющего условию
удовлетворяющего условию Следствие. Для каждого степенного ряда (2) существует число R > 0, называемое радиусом сходимости этого ряда и обладающее следующими свойствами: при при Промежуток (-R,R) называется интервалом сходимости степенного ряда(2). На концах интервала вопрос о сходимости ряда решается индивидуально для каждого конкретного ряда.
Способы определения радиуса сходимости: 1) по признаку Даламбера, 2) по радикальному признаку Коши.
|
(1) - степенной ряд
(2) – степенной ряд по степеням х.
от первого ряда можно перейти ко второму, поэтому теорию степенных рядов рассматривают для ряда(2).
, то он абсолютно
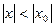. Если при
.
ряд (2) сходится абсолютно,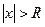
ряд (2) расходится.
