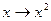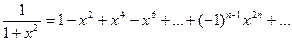Разложение ф-ций в степенные ряды. Ряд Тейлора и Маклорена
Если ф-ция f(x) является суммой ряда
то говорят что ф-ция f(x) разлагается в ряд по степеням (х – с). Важность такого разложения видна хотя бы из того, что мы получаем возможность приближенно заменить ф-цию суммой нескольких первых членов степенного ряда, т.е. многочленом.
Теорема. Если ф-ция f(x) на интервале
единственное и коэффициенты этого ряда выражаются через значения ф-ции и ее производной.
Доказательство. Дифференцируя этот ряд в интервале сходимости, получаем
При х = х0. получаем
Подставляя эти выражения для коэффициентов в формулу разложения (1), получим
Ряд в правой части равенства называется рядом Тейлора ф-ции f(x). Отметим его частный случай, когда х0 = 0:
Последний ряд называют рядом Маклорена.
Все рассуждения были сделаны в предположении, что ф-ция f(x) может быть разложена в степенной ряд. Однако, в общем случае, ряд может расходиться, и даже, если он сходится, то к другой ф-ции. Сформулируем необходимое и достаточное условие представление ф-ции степенным рядом.
Теорема. Пусть ф-ция f(x) в интервале
Из равенства
Теорема. Если в интервале
Замечание. В тех случаях, когда применение теоремы затруднительно, поступают иначе. Составив ряд Тейлора для ф-ции f(x), определяют сначала интервал его сходимости и лишь затем стараются доказать,что
Разложение в ряд Маклорена некоторых элементарных ф-ций
Эти разложения получены как непосредственным вычислением коэффициентов ряда, так и с использованием свойств почленного дифференцирования и интегрирования рядов.
1. Разложим в ряд Маклорена ф-цию Итак ряд Маклорена имеет вид Найдем производные и вычислим их в точке х=0.
Так как в любом интервале (-R,R)
2. Разложим в ряд Маклорена ф-цию Найдем производные и вычислим их в точке х=0.
Итак
3. Разложим в ряд Маклорена ф-цию Воспользуемся разложением Очевидно
4. Разложим в ряд Маклорена ф-цию Очевидно Воспользуемся разложением
Таким образом
|

 , (1)
, (1) разлагается в степенной ряд
разлагается в степенной ряд , то это разложение
, то это разложение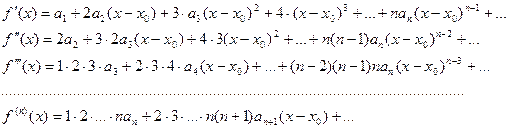




 следует, что ряд Тейлора сходится к ф-ции f(x) в интервале
следует, что ряд Тейлора сходится к ф-ции f(x) в интервале 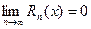 .
. , то в этом интервале ряд Тейлора для этой ф-ции сходится и его сумма равна f(x).
, то в этом интервале ряд Тейлора для этой ф-ции сходится и его сумма равна f(x).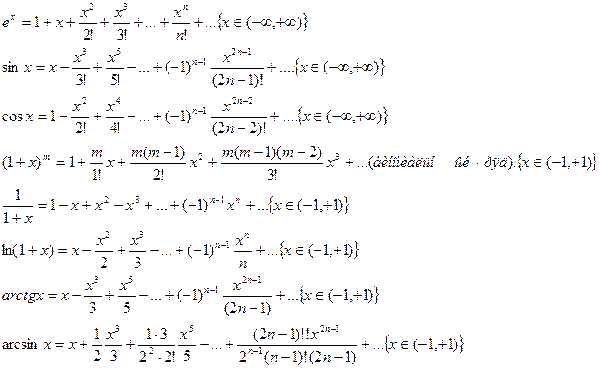
 .
. .
. , то ряд сходится к заданной ф-ции,т.е
, то ряд сходится к заданной ф-ции,т.е
 .
.

 .
.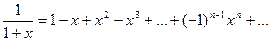 .
.
 .
.