Достаточные признаки сходимости рядов с неотрицательными членами
| Название признака
| формулировка
| Когда применяется
| | 1.Интегральный признак
Коши
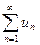|  ; un =f(n);
Если f(x) при х 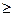 1 есть непрерывная, положительная и монотонно убывающая функция ряд 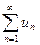сходится, если сходится несобственный интеграл  и расходится, если этот интеграл расходится.
| Для рядов типа
интегрируемых функций
| | 2. Признак сравнения 1
3. Признак сравнения 2
| Пусть даны два знакоположительных ряда
Причем 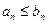 для всех n > N.
Тогда из сходимости ряда (2)  сходимость ряда (1) и из расходимости ряда (1) следует расходимость ряда (2).
Если предел отношения этих рядов существует
и конечен  , то ряды (1) и (2) ведут
себя одинаково (сходятся и расходятся одновременно).
Эталонные ряды:
1) Геометрический ряд 
2) Ряд  -  .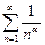
| Применяется для решения
вопроса о сходимости рядов,
для которых, используя замену
бесконечно малых величин
эквивалентными, можно
привести ряд к эталонному
| | 4. Признак Даламбера
| Если существует 
| для рядов, общие члены которых
содержат степенные, показательные
выражения и факториалы
| | 5.Радикальный признак
Коши
| Если существует
| Для рядов, общий член которых представляет собой n -ю степень выражения
|
Вычисление основной дактилоскопической формулы Вычислением основной дактоформулы обычно занимается следователь. Для этого все десять пальцев разбиваются на пять пар...
|
Расчетные и графические задания Равновесный объем - это объем, определяемый равенством спроса и предложения...
|
Кардиналистский и ординалистский подходы Кардиналистский (количественный подход) к анализу полезности основан на представлении о возможности измерения различных благ в условных единицах полезности...
|
Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями...
|
Дренирование желчных протоков Показаниями к дренированию желчных протоков являются декомпрессия на фоне внутрипротоковой гипертензии, интраоперационная холангиография, контроль за динамикой восстановления пассажа желчи в 12-перстную кишку...
Деятельность сестер милосердия общин Красного Креста ярко проявилась в период Тритоны – интервалы, в которых содержится три тона. К тритонам относятся увеличенная кварта (ув.4) и уменьшенная квинта (ум.5). Их можно построить на ступенях натурального и гармонического мажора и минора.
...
Понятие о синдроме нарушения бронхиальной проходимости и его клинические проявления Синдром нарушения бронхиальной проходимости (бронхообструктивный синдром) – это патологическое состояние...
|
Анализ микросреды предприятия Анализ микросреды направлен на анализ состояния тех составляющих внешней среды, с которыми предприятие находится в непосредственном взаимодействии...
Типы конфликтных личностей (Дж. Скотт) Дж. Г. Скотт опирается на типологию Р. М. Брансом, но дополняет её. Они убеждены в своей абсолютной правоте и хотят, чтобы...
Гносеологический оптимизм, скептицизм, агностицизм.разновидности агностицизма Позицию Агностицизм защищает и критический реализм. Один из главных представителей этого направления...
|
|
