Колебания машины
В процессе движения автомобиля толчки и удары, действующие со стороны дороги, вызывают угловые и линейные колебания подрессоренных (вес которых воспринимается рессорами) и неподрессоренных (вес которых не воспринимается рессорами) масс. Под плавностью хода понимается способность подвески поглощать толчки, удары и колебательные процессы, возникающие при движении. Плавность хода является важным эксплуатационным свойством машины, характеризующим совершенство подвески и определяющим надежность, долговечность, производительность и топливную экономичность машины, комфортабельность езды и утомляемость водителя. На плавность хода влияют: - характер микронеровностей пути; - скорость движения; - компоновка машины, конструкция и характеристики элементов подвески. Для оценки плавности хода тяговых машин выбирают оценочный параметр – критерий, характеризующий плавность хода и качество подвески, а также позволяющий сравнивать различные ее конструктивные решения и характеристики. Чем меньше значение имеет критерий, тем лучшем качеством обладает подвеска. При изучении влияния воздействий пути только на машину в качестве критерия принимают максимальное и среднее квадратичное значение абсолютных ускорений, иногда используют среднее квадратичное отклонение третий производной абсолютных перемещений, подвесочных масс. Колебания машины являются случайной функцией, поэтому и критерий плавности хода должен быть вероятностным. Иногда оценивают плавность хода по воздействию колебаний на человека. При этом характер исследования и динамический модуль путь – подвеска – машина – водитель резко усложняются и изменяют требования к параметру, применяемого в качестве критерия плавности хода. Принятый в качестве критерия плавности хода, должен отражать влияние на организм человека, характер действующих возмущений с учетом частоты процесса, амплитуды направления линейных перемещений, совместного действия линейных и угловых перемещений и явлений типа морская болезнь. Выбор параметров и проектирования подвески проводится с учетом восприятия организмом человека колебаний в определенном диапазоне частот. Известно, что при двухмассовой системе, резонансные частоты органов тела находятся в пределах 4,5…5 Гц, а при продольных колебаниях образуется дополнительный резонанс с частотой 1,8…2 Гц. Особенно плохо воспринимаются организмом человека возбуждения с частотами, близкими к резонансу органов тела. Физиологически человек привык к вертикальным колебаниям, близким по частоте колебаниям, возникающим при ходьбе, 60…100 колебаний в минуту. При частотах выше наступает неприятная тряска, а меньше частоты вызывают укачивание и даже появления симптомов морской болезни. Методы оценки влияния ускорений на организм человека сориентированы на предельно допустимые ускорения, которые испытывает человек при ходьбе. Например, при спокойной ходьбе человек испытывает 0,25g, а при спрыгивания с небольшого возвышения – 2,8…3,0g. Поэтому в качестве предельно допустимых значений ускорений рекомендуется 2,8…3,0g, а для кратковременных непрерывных воздействий – не более 1,1…1,7g. Машина в общем виде представляет собой многомассовую колебательную систему, в которой дискретные массы связаны упругими связями и имеются элементы рассеивания энергии. Такая система имеет несколько степеней свободы, но при оценки плавности хода ограничиваются рассмотрением колебаний подрессоренной массы машины в вертикальной плоскости, проходящей через плоскость продольной симметрии машины. Такие колебания называются угловыми и вертикальными плоскими колебаниями подрессоренной массы машины. В упрощенном виде при линейной характеристике упругих элементов свободные вертикальные перемещения подрессоренной массы представляет собой гармонический процесс. Частота колебаний подрессоренной массы является определяющим параметром колебательного процесса и оказывает существенное влияние на ускорение, скорость изменения ускорений и на организм человека. Для установления связи параметров рассмотрим свободные вертикальные колебания подрессоренной массы машины на схеме с одной степенью свободы при линейной характеристике упругих элементов и отсутствии рассеивания энергии в подвеске. Подрессоренная масса
где
Динамическое состояние системы представляется уравнением:
где Уравнение можно записать:
После интегрирования получим:
Определение коэффициентов А и В начальных условий приведем уравнение к виду:
где
Период колебаний:
Частота колебаний в минуту:
Выразим массу М через коэффициент жесткости и статический прогиб рессоры
Таким образом, чем мягче подвеска, тем ниже частота собственных колебаний. С коэффициентом жесткости рессор связаны дорожный просвет машины, возможный подъем колес и прогиб рессора. Дифференцированием уравнения находят: скорость колебаний:
ускорение:
скорость ускорения:
Все параметры зависят от максимальной амплитуды и угловой частоты.
|

 опирается на рессоры, приведенная жесткость которых:
опирается на рессоры, приведенная жесткость которых: ,
, - вес подрессоренной массы;
- вес подрессоренной массы; - статический прогиб рессоры.
- статический прогиб рессоры. ,
, - текущее значение отклонения масс.
- текущее значение отклонения масс. .
. .
. ,
, - максимальная амплитуда;
- максимальная амплитуда; - частота собственных колебаний.
- частота собственных колебаний.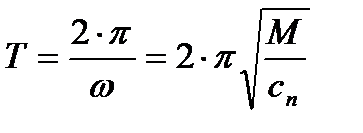 .
. .
. :
: .
. ;
; ;
; .
.


