ПЕРЕМЕННЫЙ ТОК. ПРИРОДА ЕМКОСТНЫХ СВОЙСТВ ТКАНЕЙ ОРГАНИЗМА.
1. Получение переменного тока. Основные его характеристики.
Переменным током называют ток, периодически изменяющийся по величине и направлению. Наиболее распространённым является синусоидальный переменный ток, мгновенное значение которого меняется со временем по закону синуса (или косинуса). Для получения переменного тока в технике используется возбуждение электродвижущей силы индукции в контуре, вращающемся в магнитном поле.
где S – площадь, ограниченная контуром; B – индукция магнитного поля;
где
где R – сопротивление контура и электрической цепи, в которую отводится электрический ток (посредством щёток N, скользящим по кольцам К); Im – амплитудное значение переменного тока; ω – круговая частота; Переменный ток также характеризуется периодом Т и частотой ν, причём: Для характеристики переменного тока вводится понятие действующего (эффективного) или среднеквадратичного значения тока. Эффективным или действующим значением силы переменного тока называется сила такого постоянного тока, который выделяет в данном проводнике столько же тепла за время одного периода, сколько выделяет тепла и данный переменный ток.
Приборы, включенные в цепь переменного тока (амперметр, вольтметр) показывают эффективные значения тока и напряжения.
2. Различные виды электрических сопротивлений в цепи переменного тока.
а) Активное сопротивление в цепи переменного тока.
Сопротивление R в цепи переменного тока (рис.2а) называется активным, т.к. при прохождении тока в нём происходит необратимая потеря энергии. При наличии в цепи только R напряжение
Рассмотрим случай, когда цепь содержит только катушку индуктивности с малым сопротивлением R (R=0) и значительной индуктивностью L (рис.3а). Пусть в цепи протекает переменный ток:
где где
Для цепи с индуктивностью, в которой напряжение опережает ток на 900, волновая и векторная диаграммы представлены на рис. 3б, в.
Рассмотрим случай, когда в цепь включен только конденсатор С (рис.4а) (сопротивлением и индуктивностью подводящих проводов можно пренебречь). Пусть ток в цепи изменяется по закону:
где
В цепи с чисто емкостным сопротивлением напряжение, приложенное к обкладкам конденсатора, отстаёт по фазе от тока на 900. Это отражено на волновой и векторной диаграммах на рис. 4б, в.
3. Полное сопротивление (импеданс) в цепи переменного тока.
Рассмотрим цепь, состоящую из R, L и C (рис.5а). Ток в этой цепи равен:
Вследствие наличия разности фаз между UL, UC и током I (UR находится в одинаковой фазе с током) эти напряжения можно складывать геометрически (векторно) и по теореме Пифагора получить приложенное напряжение U0 (рис.5б):
где
Разность фаз между током I и напряжением U определяется углом φ между векторами U0 и UR. Тогда: Из формулы для Z вытекает, что чем ближе по величине
4. Полное сопротивление (импеданс) тканей организма. Использование метода электропроводности в медицине.
При пропускании переменного тока через растворы их электропроводность оказывается одинаковой независимо от частоты. При работе с биологическими объектами обнаружили, что на высоких частотах (107 Гц) электропроводность гораздо выше, чем при низких частотах. С увеличением частоты электропроводность увеличивается до некоторой максимальной величины. На рис.6 (линия 1) приведена кривая зависимости сопротивления мышцы от частоты (кривая дисперсии).
По мере отмирания ткани крутизна дисперсии уменьшается и для мёртвой ткани график представляется линией 2 (рис.6). Крутизну дисперсии K выражают отношением величины сопротивления, измеренного на низкой частоте, к величине сопротивления, измеренного на высокой частоте. Если два сопротивления измеряются на разной частоте при одних и тех же условиях, то отношение между ними оказывается постоянным для нормального состояния данной ткани. Обычно выбирают для измерения частоты 104 Гц и 106 Гц, так как при частоте 106 Гц во многих случаях наблюдается максимальная электропроводность, а при частоте 104 Гц наблюдается перелом кривой дисперсии: Объясняя прохождение переменного электрического тока через биологические объекты, исходят из того, что сопротивление живых клеток является суммарным, состоящим из омического и емкостного сопротивлений. Индуктивные элементы в биологических объектах отсутствуют. Ткани организма состоят из клеток, омываемых тканевой жидкостью. Такой элемент представляет собой две среды, относительно хорошо проводящие ток (тканевая жидкость и цитоплазма клетки), разделенные плохо проводящим слоем клеточной мембраны. Такая система обладает электрической ёмкостью. В тканях встречаются и макроскопические образования, состоящие из различных соединительных оболочек и перегородок (плохо проводят ток), по обе стороны которых находятся ткани хорошо проводящие электрический ток. Это так же придаёт тканям емкостные свойства. Омическое сопротивление не зависит от частоты, а емкостное – значительно уменьшается с увеличением частоты и это приводит к увеличению проводимости всей емкостно-омической системы. Для последовательного соединения R и C полное сопротивление (импеданс) определяется по формуле: Присутствие в биологических системах ёмкостей подтверждается также наличием сдвига фаз между током и напряжением. Угол сдвига фаз определяется соотношением между емкостным и омическим сопротивлениями, и для последовательного их соединения находится по формуле: Приведём примеры величины угла сдвига фаз, полученные при частоте 103 Гц: кожа человека – 550; мышца кролика – 650; нерв лягушки – 640.

Но эти простейшие схемы не могут быть полностью применимы для живых клеток. Как следует из графика зависимости Z от ω для первой схемы (рис.7б) видно, что при частоте ω→0 сопротивление Z→∞, что противоречит опыту. Из графика зависимости Z от ω для второй схемы (рис.8б) видно, что при ω→∞ Z→0, что на опыте не подтверждается. Наиболее удачна схема, сочетающая первые две схемы. Одна из них изображена на рис.9а. На этой схеме Метод электропроводности на переменном токе в живых тканях и клетках используется в биологических исследованиях и медицине для оценки патологических процессов. Например, при измерениях в области низких частот наблюдается увеличение сопротивления ткани при воспалении на первых стадиях. Связано это с тем, что ток низкой частоты идёт преимущественно через межклеточные пространства. При воспалении в результате набухания клеток сечение межклеточных промежутков уменьшается, что влечёт повышение омического сопротивления, в то время как ёмкость клеток на ранних стадиях воспаления остаётся неизменной. В диагностике используется так же метод измерения угла сдвига фаз. При некоторых заболеваниях (щитовидной железы) или при физиологических изменениях (старение организма) обнаруживается заметное изменение угла сдвига фаз. Для характеристики физиологического состояния ткани используют величину крутизны дисперсии (K). Этот критерий применяют, например, при оценке жизнеспособности ткани, предназначенной для трансплантации. От физиологического состояния зависит так же и импеданс тканей. Так, при кровенаполнении сосудов импеданс изменяется. Кровь имеет меньшее сопротивление, чем стенки сосудов или клетки, и поэтому при наполнении ткани кровью во время систолы полное сопротивление ткани уменьшается, а при диастоле – увеличивается. Диагностический метод, основанный на регистрации импеданса тканей в процессе сердечно-сосудистой деятельности, называется реографией (импеданс – плетизмографией). С помощью этого метода получают реограммы головного мозга (реоэнцефалограмма), сердца (реокардиограмма), лёгких, печени, сосудов, конечностей. Измерения обычно проводят на частоте 30 кГц. ЛЕКЦИЯ №14
|

 Рассмотрим физические основы получения переменного тока и принцип устройства генератора. Пусть в поле постоянного магнита (B=const) вращается проводящая рамка с постоянной угловой скоростью ω (рис.1). Тогда мгновенное значение потока, связанного с контуром, будет равно:
Рассмотрим физические основы получения переменного тока и принцип устройства генератора. Пусть в поле постоянного магнита (B=const) вращается проводящая рамка с постоянной угловой скоростью ω (рис.1). Тогда мгновенное значение потока, связанного с контуром, будет равно: ,
, - угол поворота контура, отсчитанный от начального его положения, когда
- угол поворота контура, отсчитанный от начального его положения, когда  . В соответствии с законом Фарадея в рамке возникает ЭДС индукции:
. В соответствии с законом Фарадея в рамке возникает ЭДС индукции: ,
,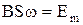 - максимальное (амплитудное) значение ЭДС индукции, т.е.
- максимальное (амплитудное) значение ЭДС индукции, т.е. 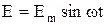 . Следовательно, если в однородном магнитном поле равномерно вращается проводящий контур, то в нём возникает переменная электродвижущая сила, изменяющаяся по закону синуса. Эта ЭДС создаёт в контуре синусоидальный переменный ток:
. Следовательно, если в однородном магнитном поле равномерно вращается проводящий контур, то в нём возникает переменная электродвижущая сила, изменяющаяся по закону синуса. Эта ЭДС создаёт в контуре синусоидальный переменный ток: ,
, . Графически значение ЭДС и переменного тока будет представляться двумя синусоидами (величины изменяются в одинаковых фазах). Рассмотренный способ получения переменного тока лежит в основе устройства промышленного генератора переменного тока. В промышленных генераторах магнитное поле создаётся мощным электромагнитом. Вращающийся контур состоит из n витков (соединённых последовательно) проволоки, намотанной на ферромагнитный сердечник (ротор генератора). Поэтому ЭДС, возбуждённая в таком генераторе будет равна:
. Графически значение ЭДС и переменного тока будет представляться двумя синусоидами (величины изменяются в одинаковых фазах). Рассмотренный способ получения переменного тока лежит в основе устройства промышленного генератора переменного тока. В промышленных генераторах магнитное поле создаётся мощным электромагнитом. Вращающийся контур состоит из n витков (соединённых последовательно) проволоки, намотанной на ферромагнитный сердечник (ротор генератора). Поэтому ЭДС, возбуждённая в таком генераторе будет равна:  .
. ,
, 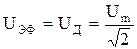 .
.
 , а
, а  , т.е. ток и напряжение совпадают по фазе. График тока и напряжения, а также векторная диаграмма амплитуд тока и напряжения показаны на рис. 2б, в.
, т.е. ток и напряжение совпадают по фазе. График тока и напряжения, а также векторная диаграмма амплитуд тока и напряжения показаны на рис. 2б, в.
 . Он вызывает в катушке ЭДС самоиндукции ЕL, которая в любой момент времени противоположна приложенному напряжению UL и уравновешивает его:
. Он вызывает в катушке ЭДС самоиндукции ЕL, которая в любой момент времени противоположна приложенному напряжению UL и уравновешивает его:  , но
, но  , тогда:
, тогда: ,
, - амплитудное значение напряжения. Из этой формулы следует, что
- амплитудное значение напряжения. Из этой формулы следует, что 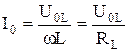 ,
, - индуктивное сопротивление катушки. Оно увеличивается с ростом частоты переменного тока. Размерность индуктивного сопротивления – Ом:
- индуктивное сопротивление катушки. Оно увеличивается с ростом частоты переменного тока. Размерность индуктивного сопротивления – Ом: ;
;  ;
;  ;
;  ;
;  .
.
 . Напряжение на обкладках конденсатора можно представить следующей формулой:
. Напряжение на обкладках конденсатора можно представить следующей формулой:  . Ток в цепи:
. Ток в цепи:  ,
,  ,
,  , тогда
, тогда ,
, - амплитудное значение напряжения, приложенного к конденсатору. Амплитудное значение тока
- амплитудное значение напряжения, приложенного к конденсатору. Амплитудное значение тока  , где
, где  - емкостное сопротивление. Оно уменьшается с ростом частоты. RC – имеет размерность – Ом:
- емкостное сопротивление. Оно уменьшается с ростом частоты. RC – имеет размерность – Ом:  ;
; ;
;  .
.
 .
. ,
, - называется полным сопротивлением, или импедансом цепи. Закон Ома для данной цепи запишется так:
- называется полным сопротивлением, или импедансом цепи. Закон Ома для данной цепи запишется так: .
. . Из диаграммы на рис.5б следует, что
. Из диаграммы на рис.5б следует, что  .
. и
и  , тем меньше полное сопротивление Z и тем больше ток в этой цепи. При RL=RC или
, тем меньше полное сопротивление Z и тем больше ток в этой цепи. При RL=RC или  полное сопротивление Z=R и ток достигает наибольшего значения, обусловленного только активным сопротивлением цепи:
полное сопротивление Z=R и ток достигает наибольшего значения, обусловленного только активным сопротивлением цепи:  . Это явление называется электрическим резонансом, который обеспечивается путём подбора соответствующих L и C. Резонанс в последовательной цепи называют резонансом напряжений, так как при этом происходит взаимная компенсация напряжений UL и UC (направлены противоположно), каждое из которых порознь может значительно превышать напряжение U, приложенное к цепи.
. Это явление называется электрическим резонансом, который обеспечивается путём подбора соответствующих L и C. Резонанс в последовательной цепи называют резонансом напряжений, так как при этом происходит взаимная компенсация напряжений UL и UC (направлены противоположно), каждое из которых порознь может значительно превышать напряжение U, приложенное к цепи. Зона дисперсии электропроводности обычно варьируется в интервале 102 – 108 Гц. Дисперсия электропроводности живых тканей является результатом того, что при низких частотах, как и при постоянном токе, электропроводность связана с поляризацией, но по мере увеличения частоты поляризационные явления сказываются меньше.
Зона дисперсии электропроводности обычно варьируется в интервале 102 – 108 Гц. Дисперсия электропроводности живых тканей является результатом того, что при низких частотах, как и при постоянном токе, электропроводность связана с поляризацией, но по мере увеличения частоты поляризационные явления сказываются меньше. . После отмирания ткани указанный коэффициент стремится к единице.
. После отмирания ткани указанный коэффициент стремится к единице. .
. . Для биологических систем характерна большая величина этого угла. Это показывает, что доля емкостного сопротивления в тканях велика.
. Для биологических систем характерна большая величина этого угла. Это показывает, что доля емкостного сопротивления в тканях велика.
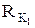 и
и  - сопротивление кожи; RT – сопротивление ткани; C1, C2 и C3 – шунтирующие эти сопротивления ёмкости. Стрелками показано направление переменного тока в один из полупериодов. Сопротивления
- сопротивление кожи; RT – сопротивление ткани; C1, C2 и C3 – шунтирующие эти сопротивления ёмкости. Стрелками показано направление переменного тока в один из полупериодов. Сопротивления 


