Предел последовательности.
Опр.1. Пусть 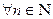 поставлено в соответствие вполне определенное число a
поставлено в соответствие вполне определенное число a 
 (причем различным n могут соответствовать одинаковые числа). Совокупность элементов a
(причем различным n могут соответствовать одинаковые числа). Совокупность элементов a  , n=1,2,3… называется числовой последовательностью, каждый элемент a
, n=1,2,3… называется числовой последовательностью, каждый элемент a  - элементом (членом) последовательности, n-его номер.
- элементом (членом) последовательности, n-его номер.
Опр.2. Число 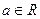 называется пределом последовательности
называется пределом последовательности 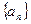 ,
, 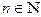 , если для любого сколь угодно малого действительного положительного
, если для любого сколь угодно малого действительного положительного 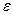 , найдется такой номер
, найдется такой номер 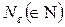 , зависящий от
, зависящий от 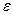 , что | a
, что | a  - a |<
- a |< 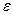 при
при 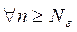 .В этом случае пишут
.В этом случае пишут  а
а  = а или а
= а или а 
 а при n
а при n 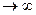 .
.
Опр.3. Последовательность 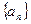 , n
, n 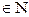 ,называется ограниченной, если существует действительное число с>0, что | a
,называется ограниченной, если существует действительное число с>0, что | a  |<c при
|<c при  .
.
Пример 1. Зная несколько первых членов последовательности, написать одно из возможных выражений для общего члена:
 ;
; 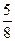 ;
; 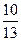 ;
; 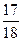 ;
;  ;…
;…
Решение: числитель каждого из заданных членов последовательности равен квадрату номера этого члена плюс единица, т.е. n  +1. Знаменатели образуют арифметическую прогрессию 3,8,13,18…. с первым членом x
+1. Знаменатели образуют арифметическую прогрессию 3,8,13,18…. с первым членом x  =3 и разностью d=5. Поэтому x
=3 и разностью d=5. Поэтому x  =x
=x  +d(n-1)=5n-2.
+d(n-1)=5n-2.
Следовательно, исходная формула а  =
=  .
.
ЗАМЕЧАНИЕ: знание нескольких первых членов последовательности еще не определяет эту последовательность.
Пример 2. Доказать, что последовательность а  =(-1)
=(-1) 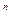
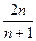 sin n ограничена.
sin n ограничена.
Решение: | а  |=|(-1)
|=|(-1) 
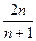 sin n|=|(-1)
sin n|=|(-1)  | |
| | 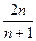 | |sin n|
| |sin n| 
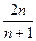 =2-
=2- 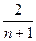 <2,
<2, 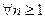
Отсюда, по опр.3. а  -ограничена, с=2.
-ограничена, с=2.
Пример 3. Непосредственно доказать, что при  ,
,
Решение: Необходимо доказать, что 
Пример 4. Пользуясь опр.2., доказать, что  а
а  =
= 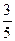 , если а
, если а  =
=  , начиная с какого n выполняется неравенство
, начиная с какого n выполняется неравенство
| а  -
- 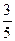 | <0,01.
| <0,01.
Решение: найдем | а  -
- 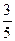 | = |
| = |  -
- 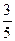 | =
| = 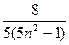 .
.
Пусть 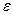 >0 задано. Выберем так, чтобы выполнялось неравенство
>0 задано. Выберем так, чтобы выполнялось неравенство 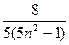 <
< 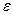 .
.
Решаем это неравенство: в силу 17  действительных чисел, будем иметь 5
действительных чисел, будем иметь 5  -1>
-1> 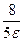
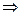
 >
> 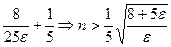 .
.
Положив  = [
= [  ]+1, получим, что при
]+1, получим, что при 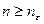 , | a
, | a 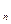 -
- 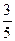 |<
|< 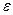 .
.
А это означает в силу опр.2.  а
а 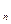 =
= 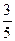 . Пусть
. Пусть 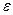 =0,01, тогда n
=0,01, тогда n  =[
=[  ]+1= [
]+1= [  ]+1=6 и все члены последовательности, начиная с шестого, содержатся в U(
]+1=6 и все члены последовательности, начиная с шестого, содержатся в U(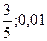 ) – окрестности точки
) – окрестности точки 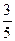 , т.е. в интервале ]
, т.е. в интервале ]  [ =]0,59;0,61[.
[ =]0,59;0,61[.
ВАРИАНТЫ.
1.Найти 4-первых члена последовательности, если дана формула общего члена:
1) a  =sin (
=sin ( ) 2)
) 2) 
3) 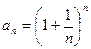 4)
4) 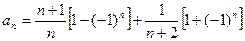
5) 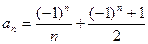 6)
6) 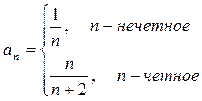
7)  8)
8) 
9) 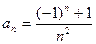 10)
10) 
11)  12)
12) 
13) 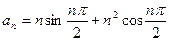 14)
14) 
15) 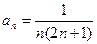 16)
16) 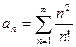
17)  18)
18) 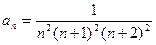
19) 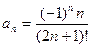 20)
20) 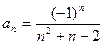
21) 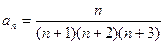 22)
22) 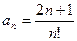
23) 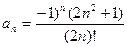 24)
24) 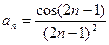
25) 
2. Зная несколько первых членов последовательности, написать одно из возможных выражений для общего члена:
1) 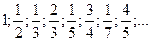 2)
2) 
3) 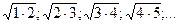 4)
4) 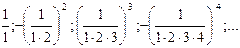
5) 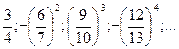 6)
6) 
7) 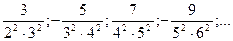 8)
8) 
9) 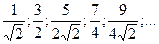 10)
10) 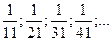
11)  12)
12) 
13)  14)
14) 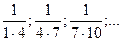
15)  16)
16) 
17) 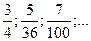 18)
18) 
19) 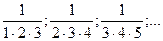 20)
20) 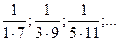
21) 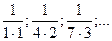 22)
22) 
23) 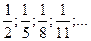 24)
24) 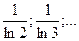
25) 
3. Доказать ограниченность последовательности:
1) a  =
= 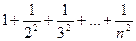 ;
;
2) a  =
=  ;
;
3) a  =
= 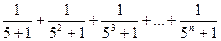 ;
;
4) a  =
=  ;
;
5) a  =
= 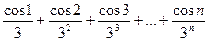 ;
;
6) a  =
= 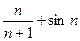 ;
;
7) a  =
= 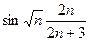 ;
;
8) a  =
= 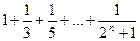 ;
;
9)  ;
;
10) 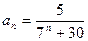 ;
;
11)  ;
;
12) 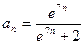 ;
;
13)  ;
;
14) an =sin n + 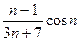 ;
;
15)  ;
;
16)  ;
;
17) 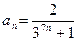 ;
;
18) 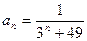 ;
;
19) 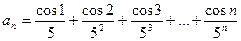 ;
;
20) 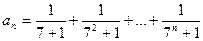 ;
;
21)  ;
;
22)  ;
;
23)  ;
;
24)  ;
;
25)  ;
;
4. Пользуясь опр.2. доказать, что  . Начиная с какого n выполняется неравенство | a
. Начиная с какого n выполняется неравенство | a 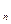 - a | < 0,01:
- a | < 0,01:
1) a  =
=  , а =0 2) a
, а =0 2) a  =
=  , а =3
, а =3
3) a  =
= 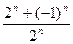 , а =1 4) a
, а =1 4) a  =
= 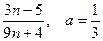
5) a  =
= 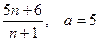 6) a
6) a  =
= 
7) a  =
=  8) a
8) a  =
= 
9) 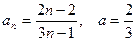 10)
10) 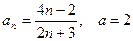
11)  12)
12) 
13) 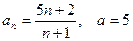 14)
14) 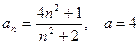
15) 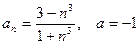 16)
16) 
17) 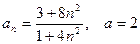 18)
18) 
19)  20)
20) 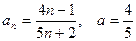
21)  22)
22) 
23)  24)
24) 
25) 

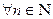 поставлено в соответствие вполне определенное число a
поставлено в соответствие вполне определенное число a 
 (причем различным n могут соответствовать одинаковые числа). Совокупность элементов a
(причем различным n могут соответствовать одинаковые числа). Совокупность элементов a 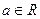 называется пределом последовательности
называется пределом последовательности 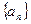 ,
, 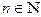 , если для любого сколь угодно малого действительного положительного
, если для любого сколь угодно малого действительного положительного 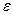 , найдется такой номер
, найдется такой номер 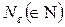 , зависящий от
, зависящий от 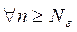 .В этом случае пишут
.В этом случае пишут  а
а  а при n
а при n 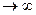 .
.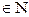 ,называется ограниченной, если существует действительное число с>0, что | a
,называется ограниченной, если существует действительное число с>0, что | a  .
. ;
; 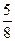 ;
; 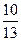 ;
; 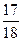 ;
;  ;…
;… +1. Знаменатели образуют арифметическую прогрессию 3,8,13,18…. с первым членом x
+1. Знаменатели образуют арифметическую прогрессию 3,8,13,18…. с первым членом x  =3 и разностью d=5. Поэтому x
=3 и разностью d=5. Поэтому x  .
.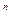
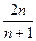 sin n ограничена.
sin n ограничена.
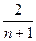 <2,
<2, 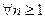
 ,
, а
а 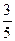 , если а
, если а  , начиная с какого n выполняется неравенство
, начиная с какого n выполняется неравенство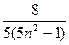 .
. действительных чисел, будем иметь 5
действительных чисел, будем иметь 5  -1>
-1> 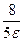
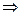
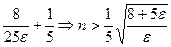 .
. = [
= [  ]+1, получим, что при
]+1, получим, что при 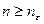 , | a
, | a 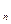 -
- 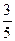 |<
|< 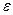 .
. а
а  =[
=[  ]+1= [
]+1= [  ]+1=6 и все члены последовательности, начиная с шестого, содержатся в U(
]+1=6 и все члены последовательности, начиная с шестого, содержатся в U(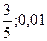 ) – окрестности точки
) – окрестности точки  [ =]0,59;0,61[.
[ =]0,59;0,61[. =sin (
=sin ( ) 2)
) 2) 
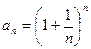 4)
4) 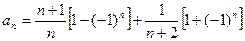
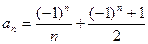 6)
6) 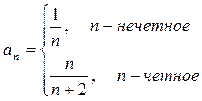
 8)
8) 
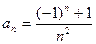 10)
10) 
 12)
12) 
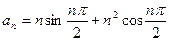 14)
14) 
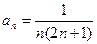 16)
16) 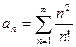
 18)
18) 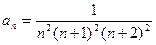
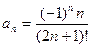 20)
20) 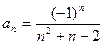
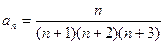 22)
22) 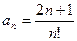
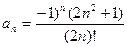 24)
24) 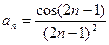

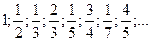 2)
2) 
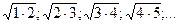 4)
4) 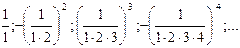
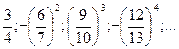 6)
6) 
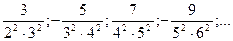 8)
8) 
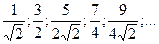 10)
10) 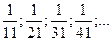
 12)
12) 
 14)
14) 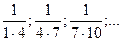
 16)
16) 
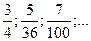 18)
18) 
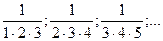 20)
20) 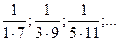
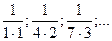 22)
22) 
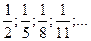 24)
24) 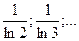

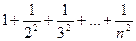 ;
; ;
;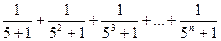 ;
; ;
;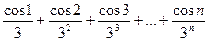 ;
;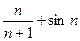 ;
;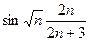 ;
;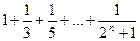 ;
; ;
;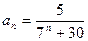 ;
; ;
;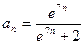 ;
; ;
;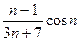 ;
; ;
; ;
;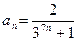 ;
;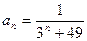 ;
;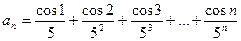 ;
;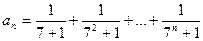 ;
; ;
; ;
; ;
; ;
; . Начиная с какого n выполняется неравенство | a
. Начиная с какого n выполняется неравенство | a  , а =0 2) a
, а =0 2) a  , а =3
, а =3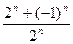 , а =1 4) a
, а =1 4) a 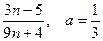
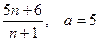 6) a
6) a 
 8) a
8) a 
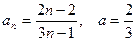 10)
10) 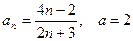
 12)
12) 
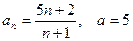 14)
14) 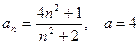
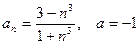 16)
16) 
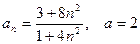 18)
18) 
 20)
20) 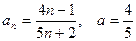
 22)
22) 
 24)
24) 




