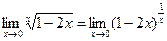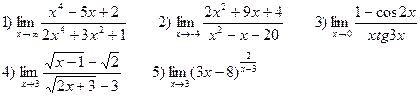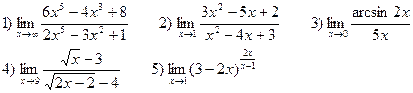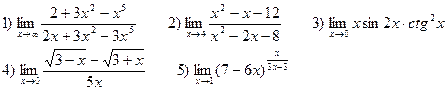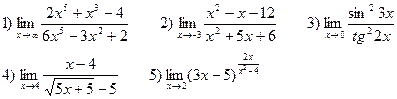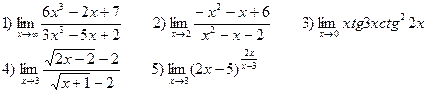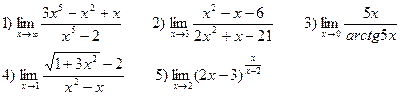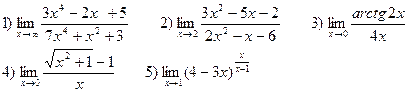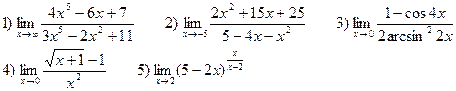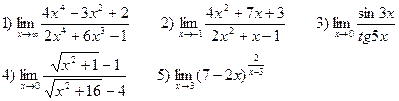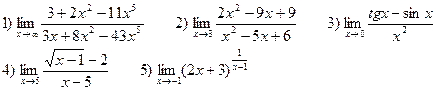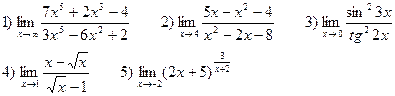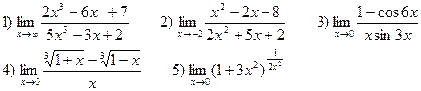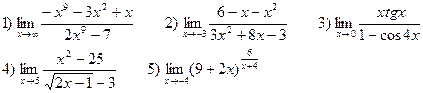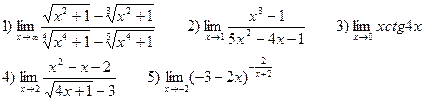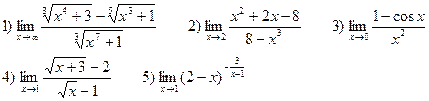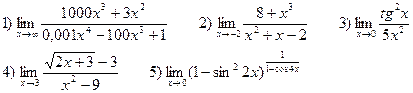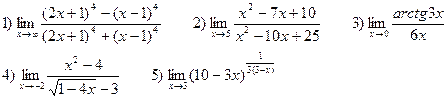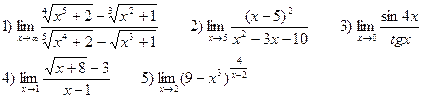ЛАБОРАТОРНАЯ РАБОТА №6
Вычисление предела функции. При вычислении предела функции необходимо знать следующие теоремы:
Кроме того, надо пользоваться тем, что для всех основных элементарных функций в любой точке их области определения справедливо равенство:
Этими простейшими пределами можно пользоваться как формулами:
Более сложные случаи нахождения предела функции: Пример 1. Найти предел:
Решение:
Разлагаем знаменатель на множители:
Здесь нет сокращения на нуль, что никогда недопустимо. Согласно определению предела функции аргумент х стремиться к своему предельному значению 2, никогда с ним не совпадая. Пример 2. Найти предел:
Решение:
Решение:
(Применяем тригонометрическую формулу так, чтобы использовать первый замечательный предел).
Пример 4. Найти предел:
Решение:
Деля числитель и знаменатель на наивысшую степень х (на х2), находим
Случай, когда при х® а или х®¥ функция f (x) представляет произведение бесконечно малой величины на бесконечно большую Случай, когда при х® а или х®¥ функция f (x) представляет разность двух положительных бесконечно больших величин Пример 5. Найти следующий предел:
Решение:
ВАРИАНТЫ. Найти следующие пределы: В-1
В-2
В-3
В-4
В-5
В-6
В-7
В-8
В-9
В-10
В-11
В-12
В-13
В-14
В-15
В-16
В-17
В-18
В-19
В-20
В-21
В-22
В-23
В-24
В-25
|
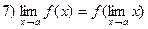(в силу непрерывности, Л.р. №7)
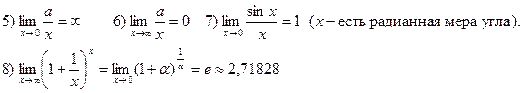
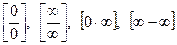,[1¥] рассматриваются далее в отдельности.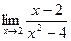
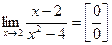
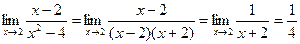
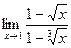
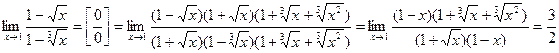Пример 3. Найти предел: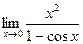
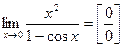
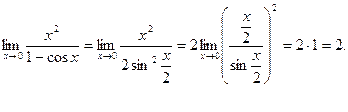
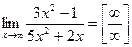
, приводится путем преобразования функции к одному из двух рассмотренных случаев, т.е. к 
или к 
.
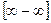, можно привести к случаю 
