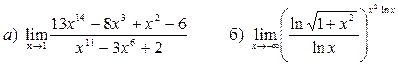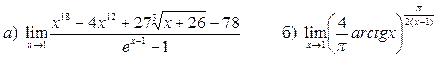Неопределенность . По правилу Лопиталя данный предел равен
В этом примере однократное применение правила Лопиталя снимает неопределенность. Пример 2. Найти Решение: Неопределенность
что снова приводит к неопределенности
Здесь правило Лопиталя применимо дважды. Пример 3. Вычислить Решение: Неопределенность
Здесь правило Лопиталя применимо п раз. II. Случай нахождения предела:
III. Случай нахождения предела:
Замечание: Эти случаи нахождения предела функции сводятся к случаям Пример 4. Найти пределы: а) Решение: Установив, что имеет место случай а) б) 1) 2) 3) Замечание: Эти случаи нахождения предела функции также сводятся к случаям Пример 6. Найти Решение: 1) Сначала устанавливаем, что имеет место случай 2) Затем логарифмируем функцию и ищем предел её логарифма:
3) здесь нахождение предела свелось к случаю Применяя правило Лопиталя, получим
4) Теперь по найденному пределу логарифма функции находим искомый предел самой функции
ВАРИАНТЫ. Вычислить: В-1
В-2
В-3
В-4
В-5
В-6
В-7
В-8
В-9
В-10
В-11
В-12
В-13
В-14
В-15
В-16
В-17
В-18
В-19
В-20
В-21
В-22
В-23
В-24
В-25
ЛИТЕРАТУРА: 1) Зорич В.А. Математический анализ. Ч-I-М.: Наука, 1981 2) Ильин В.А., Позняк Э.Г. Основы математического анализа. Ч.-I –М.: Наука, 1971 3) Фихтенгольц Г.И. Курс дифференциального и интегрального исчисления, Т. 1,2,3. –М.: Наука, 1969 4) Кудрявцев Л.Д. Курс математического анализа, Т. I – М.: Высшая школа, 1981 5) Данко П.Е., Кожевникова Т.Я. Высшая математика в упражнениях и задачах: Учебное пособие для студентов ВТУЗов. В двух частях. Ч.I. М.: Высшая школа, 1986 6) Справочное пособие по математическому анализу. Ч.I: Введение в анализ, производная, интеграл /Ляшко И.И., Боярчук А.К., Гай и др. Киев, ВШ, 1978 7) Ильин В.А.,Сендов Бл.Х.,Садовничий В.А. Математический анализ, Т. 1,2,3. – М.: Изд-во МГУ, 1985 8) Никольский С.М. Курс математического анализа. Т. 1,2. М.: Наука, 1983. 9) Демидович Б.П. Сборник задач и упражнений по математическому анализу: Учебное пособие для ВУЗов. М.: АСТ Астрель, 2003. 10)Гусак А.А. Задачи и упражнения по высшей математике: Учебное пособие для ВУЗов. Ч.1,2. Минск: Высшая школа, 1988
|



 . По правилу Лопиталя данный предел равен
. По правилу Лопиталя данный предел равен


 . По правилу Лопиталя данный предел равен
. По правилу Лопиталя данный предел равен
 - когда функция представляет произведение бесконечно малой величины на бесконечно большую.
- когда функция представляет произведение бесконечно малой величины на бесконечно большую.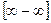 - когда функция представляет разность двух положительных бесконечно больших величин.
- когда функция представляет разность двух положительных бесконечно больших величин. б)
б) 

 III. Случаи нахождения предела:
III. Случаи нахождения предела: - когда функция представляет степень, основание которой стремится к единице, а показатель к бесконечности.
- когда функция представляет степень, основание которой стремится к единице, а показатель к бесконечности. - когда функция представляет степень, основание которой стремится к бесконечности, а показатель к нулю.
- когда функция представляет степень, основание которой стремится к бесконечности, а показатель к нулю. - когда функция представляет степень, основание и показатель которой стремятся к нулю.
- когда функция представляет степень, основание и показатель которой стремятся к нулю.

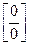 .
.