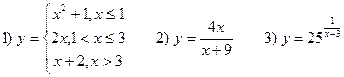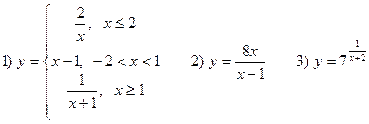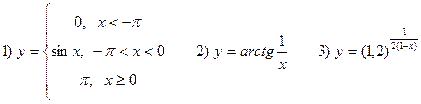ЛАБОРАТОРНАЯ РАБОТА № 7.
Непрерывность и точки разрыва функции. Если ищется предел функции
Аналогично можно сформулировать определение правостороннего (правого) предела данной функции, который обозначается так:
Теорема. Функция 1) функция 2)функция 3)односторонние пределы при
Если для данной функции Локальные свойства. Локальными называют такие свойства функций, которые определяются поведением функции в сколь угодно малой окрестности точки области определения. Теорема. Пусть 10 Функция 20 Если 30 Если функция a) b) c) 40 Если функция
Опр.1. Если точка разрыва Опр.2. Разрыв функции Опр.3. Скачком функции в точке разрыва называется абсолютная величина разности между ее правым и левым предельными значениями. Пример 1. Функция
Решение: Данная функция определена и непрерывна в интервалах (-¥,2), (-2,1), (1,+¥),т.к. постоянная и непрерывная функции непрерывны на всей действительной оси. При х=-2 и х=1 меняется аналитическое выражение функции, и только в этих точках функция может иметь разрыв. Определим односторонние пределы в точке х=-2:
Односторонние пределы совпадают. Функция в этой точке непрерывна Определим односторонние пределы в точке х=1:
Т.к. односторонние пределы функции у=f(x) в точке х=1 не равны между собой, то в этой точке функция имеет разрыв первого рода. В точке х=1 скачок функции имеет значение, равное D=|2-(-3)|=5. График функции показан на рис.1.
Пример 2. Дана функция Решение: Наша функция является отношение 2-х линейных функций, которое является непрерывным на всей действительной оси. Значит исходная функция непрерывна всюду на действительной оси, кроме (×) x=2. При х=-2 данная функция не существует; в этой точке функция терпит разрыв. Определим односторонние пределы функции при х®-2 слева и справа:
Таким образом, при х=-2 данная функция имеет разрыв второго рода. ВАРИАНТЫ. Дана функция, найти точки разрыва функции и построить график: В-1
В-2
В-3
В-4
В-5
В-6
В-7
В-8
В-9
В-10
В-11
В-12
В-13
В-14
В-15
В-16
В-17
В-18
В-19
В-20
В-21
В-22
В-23
В-24
В-25
|

 при условии, что аргумент
при условии, что аргумент  , стремясь к своему предельному значению а, может принимать только такие значения, которые меньше а, то этот предел, если он существует, называется левосторонним (левым) пределом данной функции в точке
, стремясь к своему предельному значению а, может принимать только такие значения, которые меньше а, то этот предел, если он существует, называется левосторонним (левым) пределом данной функции в точке  =
= 
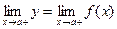 =
= 

 –функция, непрерывная в точке а. Тогда справедливы следующие утверждения:
–функция, непрерывная в точке а. Тогда справедливы следующие утверждения: ограничена в некоторой окрестности
ограничена в некоторой окрестности  точки а.
точки а. ,то в некоторой окрестности
,то в некоторой окрестности  .
. определена в некоторой окрестности точки а и,как и
определена в некоторой окрестности точки а и,как и  ,
, ,
,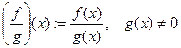 , определены в некоторой окрестности точки а и непрерывны в точке а.
, определены в некоторой окрестности точки а и непрерывны в точке а. непрерывна в точке b, а функция
непрерывна в точке b, а функция  такова что
такова что  и
и 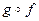 определена на
определена на  и также непрерывна в точке а.
и также непрерывна в точке а. функции
функции  , но
, но  , то
, то 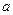 называется точкой устранимого разрыва функции
называется точкой устранимого разрыва функции 


 рис.1.
рис.1. . Найти точки разрыва функции, если они существуют. Построить график функции.
. Найти точки разрыва функции, если они существуют. Построить график функции.