ЛАБОРАТОРНАЯ РАБОТА № 4. Вычисление предела последовательности.
Вычисление предела последовательности. Числовая последовательность не может иметь более одного предела. Последовательность, имеющая предел, называется сходящейся. Для сходящихся последовательностей справедливы теоремы, вытекающие из определения предела: 1. 2. 3. Пример 1. Найти предел: Как показывает решение задачи, подстановка предельного значения приводит к неопределенности Решение примера 1: Поделим числитель и знаменатель на наивысшую степень n, в данном случае на n
Т.к. Пример 2. Найти предел: Решение: Умножим и разделим выражение, стоящее под знаком предела на выражение сопряженное ему:
Пример 3. Найти предел: Решение: Воспользуемся 2-м замечательным пределом: = ВАРИАНТЫ. Найти следующие пределы. В-1 1) 5) В-2 1) 3) 5) В-3 1) 3) 5) В-4 1) 3) 5) В-5 1) 3) 5) В-6 1) 3) 5) В-7 1) 3) 5) В-8 1) 3) 5) В-9 1) 3) 5) В-10 1) 3) 5) В-11 1) 3) 5) В-12 1) 3) 5) В-13 1) 3) 5) В-14 1) 3) 5) В-15 1) 3) 5) В-16 1) 3) 5) В-17 1) 3) 5) В-18 1) 3) 5) В-19 1) 3) 5) В-20 1) 3) 5) В-21
1) 3) 5) В-22 1) 3) 5) В-23 1) 3) 5) В-24 1) 3) 5) В-25 1) 3) 5)
|





 . Часто встречаются неопределенности вида
. Часто встречаются неопределенности вида  . Нахождение предела последовательности в этих случаях называют раскрытием неопределенности. Для раскрытия неопределенности приходится, прежде чем перейти к пределу, проводить преобразования данного выражения.
. Нахождение предела последовательности в этих случаях называют раскрытием неопределенности. Для раскрытия неопределенности приходится, прежде чем перейти к пределу, проводить преобразования данного выражения. :
: .
. (см. пр.3 Л.р.№3).
(см. пр.3 Л.р.№3).
 .
.


 .
.
 2)
2)  3)
3)  4)
4) 

 2)
2) 
 4)
4) 

 2)
2) 
 4)
4) 

 2)
2) 
 4)
4) 

 2)
2) 
 4)
4) 

 2)
2) 
 4)
4) 

 2)
2) 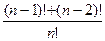
 4)
4) 

 2)
2) 
 4)
4) 

 2)
2) 
 4)
4) 

 2)
2) 
 4)
4) 

 2)
2) 
 4)
4) 

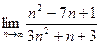 2)
2) 
 4)
4) 

 2)
2) 
 4)
4) 

 2)
2) 
 4)
4) 

 2)
2) 
 4)
4) 

 2)
2) 
 4)
4) 

 2)
2) 
 4)
4) 

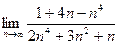 2)
2) 
 4)
4) 

 2)
2) 
 4)
4) 

 2)
2) 
 4)
4) 

 2)
2) 
 4)
4) 

 2)
2) 
 4)
4) 

 2)
2) 
 4)
4) 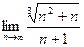

 2)
2) 
 4)
4) 

 2)
2) 
 4)
4) 




