Види понять.
Важливою проблемою логіки є класифікація понять, завдяки якій вони систематизуються. Наслідком цього є мислене упорядкування предметного світу, орієнтованого на його об’єктивну упорядкованість. Якщо складові обсягу поняття не можуть бути частинами змісту інших понять, то вони називаються індивідуумами, а в протилежному випадку – видами. Найбільша відмінність існує між тими поняттями, в яких відображаються реально існуючі (чи ті, що існували) предмети, і тими, в яких мисляться уявні предмети, – так званими нульовими поняттями. Останні ще називають поняттями з пустим обсягом або просто – пустими, а протилежні – непустими. Непусте поняття – поняття, в якому мисляться реально існуючі (або ті, що існували) предмети. Наприклад: “Токіо”, “Карфаген”, “Ярослав Мудрий”, “океан”, “слон”, “мамонт”. Пусте поняття – поняття, в якому мисляться предмети, котрих або ще не було й немає, або ніколи не буде. Наприклад: “людина, яка побувала на Марсі”, “лікар, який здатний перемогти ракову хворобу на будь-якій стадії її розвитку”, “вічний двигун”, “античне божество”, “абсолютно чорне тіло”. Варто підкреслити, що не тільки не пусті, а й пусті поняття поділяються за обсягом і змістом. За обсягом, тобто за кількістю предметів, які в них мисляться, поняття поділяються на загальні і одиничні. Загальне поняття – поняття, в якому мислиться два чи більше предметів. Наприклад: “полюс Землі”, “планета сонячної системи”, “елементарна частка”, “відьма”, “вічний двигун”. Одиничне поняття – поняття, в якому мислиться один-єдиний предмет. Наприклад: “найдовша на Землі ріка”, “Чернівецький державний університет”, “найповноводніша ріка на Місяці”, “Г.Сковорода”. Усі поняття, незалежно від того, до якого з перелічених видів і підвидів вони належать, поділяються на збірні і незбірні. Збірне поняття – поняття, в якому кожен елемент обсягу є сукупністю відносно самостійних предметів, що мисляться як один предмет (“сузір’я”, “сузір’я Водолія”, “оркестр ХХІ ст.”). Всі інші належать до незбірних. Обравши відповідну основу поділу, перелічені види понять, у свою чергу можна поділити на підвиди. Так загальні поняття поділяють на реєструючи та нереєструючі. Основою цього поділу є наявність або відсутність у побічній частині змісту поняття таких ознак, які відповідають на запитання: “де?”, “коли?”, “якого роду індивідуум?”. Якщо у змісті поняття є ознаки, що відповідають на названі запитання, то вони називаються реєструючими, а в зворотньому випадку – нереєструючими. Реєструючі поняття – це поняття, в обсязі яких мислиться скінченна, обчислювана множина предметів. Наприклад: “пора року”, “обласний центр України”, “чорне море”, “Т.Г.Шевченко”, “населення України”. Поняття цього виду визначені не тільки якісно, за допомогою частини ознак їх змісту визначаються так чи інакше і чисельність мислимих предметів, які виділяються із загального числа предметів, що мають якісну визначеність, представлену головною частиною цього поняття. Нереєструючі поняття – це поняття, обсяг яких не піддається обчисленню. Наприклад: “елементарна частка”, “небесне тіло”, “людство”, “квіти”, “рослини”, “відданість”, “слово”. Ці поняття визначаються лише якісно: в них немає ознак, які виділяють у класі предметів певну якісну означеність будь-якої її частини шляхом фіксування просторових або часових меж чи шляхом посилання на одиничність предмета. Тому ці поняття іноді називаються відкритими, на відміну від реєстраційних понять, які часто називають закритими. Для позначення відкритого поняття застосовується символ Аbc, а для позначення закритого (реєструючого) – символ (Аbc). Одиничне реєструюче поняття позначається символом О(Аbc), а множинне реєструюче поняття – символом М(Аbc). Залежно від того, мисляться в поняттях ознаки з їх носіями (предметами) чи ізольовано від них, вони поділяються на конкретні і абстрактні. Конкретне поняття – поняття, в якому мисляться ознаки з їх носіями, тобто відповідними предметами. Наприклад: “машина”, “людина”, “тварина”. Абстрактне поняття – поняття, в якому мислиться ознака, ізольована від її носія. Наприклад: “мужність”, “хоробрість”, “світлість”, “темрява”. Так, у понятті “геніальна людина” мисляться і ознаки, притаманні геніальним людям, і носії цих ознак – геніальні люди, а в понятті “геніальність” відповідна ознака відділяється свідомістю від її носія і мислиться як щось окреме, як самостійний предмет думки (як це парадоксально не звучить). Тому поняття “геніальна людина” належить до конкретних, а “геніальність” – до абстрактних. Поняття ще поділяються на позитивні і негативні. Позитивне поняття – поняття, в якому виражається наявність у предмета певних ознак. Наприклад: “добрий”, “красивий”, “скупий”. Негативне (заперечне) поняття – поняття, в якому виражається відсутність у предмета ознак, що становлять зміст відповідного позитивного поняття. Наприклад: “недобрий”, “некрасивий”, “нескупий”. Зміст негативного поняття не можна визначити без знання змісту відповідного йому позитивного (“люди” – “нелюди”, “ссавці” – “не ссавці”). В одних і тих самих поняттях одночасно відображаються і предмети, і їх зв’язки зі світом. Про це свідчить хоча б наявність у змісті переважної більшості понять родових ознак, характерних для кожного елемента їх обсягу. Проте у формальній логіці до певної міри абстрагуються від цієї істини, жорстоко поділяючи поняття на абсолютні (безвідносні) і відносні (співвідносні). Абсолютне поняття – поняття, що відображає предмет, з існуванням якого не пов’язується необхідне існування будь-яких інших предметів. Наприклад: “наука”, “культура”, “мистецтво”, “прокурор”, “дерево”, “прислівник”. Відносне поняття – поняття, що відображає предмети, існування яких немислиме без існування деяких інших предметів. Наприклад: “дружина”, “чоловік”, “вчитель”, “учень”, “мати”, “сват”, “командир”. Види понять наведено в таблиці №2 (до лекції №2). 4.Узагальнення і обмеження понять. Обмеження поняття – логічна операція над поняттями, завдяки якій відбувається перехід від поняття з ширшим обсягом (родового) до поняття з вужчим обсягом (видового) через додавання до змісту вихідного поняття ознак, які стосуються лише частини предметів його обсягу. Наприклад: “ держава” – “європейська держава ” – “Українська держава”. Обмежувати поняття можна до індивідуальних (одиничних) понять, бо далі буде вже не обмеження, а розчленування цілого на частини, оскільки обсяг одиничних понять складається лише з одного елемента. Узагальнення поняття – логічна операція, в результаті якої відбувається перехід від поняття з вужчим обсягом (видового) до поняття з ширшим обсягом (родового) шляхом збіднення його змісту, тобто вилучення специфічних для вихідного поняття видових ознак. Наприклад: ”Маріупольський державний університет” – “університет” – “вищий навчальний заклад” – “ заклад”. Межею узагальнення є гранично широкі за обсягом поняття, які називають категоріями. Кожна наука має свої категорії, тобто найзагальніші в ній поняття. Операції обмеження й узагальнення можна передати з допомогою схеми (схема 1, буквами а, b, с позначено ознаки, які віднімаються при узагальненні і додаються при обмеженні поняття). Діаграма обмеження і узагальнення понять (див. схема 1 до лекції №2). Іноді логічні операції обмеження й узагальнення понять важко відрізнити від інших операцій. Треба зазначити, що вони використовуються лише тоді, коли відбувається перехід від родового поняття до видового (обмеження), або від видового до родового (узагальнення). Іншими словами обмеження або узагальнення мають місце лише в тому разі, коли вихідне поняття і те, яке утворюється внаслідок цих логічних операцій, перебувають у відношенні підпорядкування. Так, перехід від поняття “корінь слова” до поняття “основа слова” може здатися узагальненням. Проте це не відповідає дійсності, оскільки названі поняття перехресні. Не належить до узагальнення і перехід від поняття “дерево” до поняття “гай”, оскільки ці поняття навіть не сумісні: жодне дерево не є гаєм і навпаки.
v Висновки: Поняття є найпростішою і фундаментальною формою мислення. Воно призначене для номінування предметів чи їх різноманітних якостей. Базовими характеристиками поняття є об’єм та зміст, за якими поняття класифікують на види. За об’ємом поняття можна обмежувати та узагальнювати, переводячи родові поняття у видові і навпаки. Між поняттями за певних умов бувають відносини відносин сумісності чи несумісності. v Питання для самоконтролю за темою 2: 1. Що таке поняття, наведить приклади. 2. Що таке обмеження і узагальнення поняття? Наведіть самостійні приклади. 3. Які базові характеристики існують у понятті, розкрийте їх суть. 4. Які ознаки понять Ви можете назвати? Яку роль виконують ознаки у створенні понять? 5. Назвіть види понятть. 6. Поясність відмінність між конкретними і абстрактними поняттями.
Тема 3. Логічні відношення та операції над поняттями. План. 1. Відношення між поняттями. 2. Операції над поняттями, їх классами. 3. Визначення понять. Література. 1. Бойко А. П. Формально-логические основы классификации // Логические проблемы исследования научного познания. — М., 1980. 2. Маковельский А. О. История логики. — М., 1967. 3. Тофтул М.Г. Логіка, К., 1999. 4. В.Х.Арутюнов, В.М.Мішин, Д.П.Кирик Логіка, К., 2000. 5. І.В.Хоменко, І.А.Алексюк Основи логіки К., 1996. 6. В.И.Кирилов, А.А.Старченко Логика, М., 1995. v Мета:дати уявлення про відношення між поняттями (відношення тотожності; відношення підпорядкування, відношення перетину); розглянути операції над поняттями (додавання, множення, віднімання, операція доповнення обсягів понятть), визначити правила визначення понять.
v Ключові поняття та терміни:порівнянні поняття, непорівнянні поняття, сумісні поняття, несумісні поняття, дефініція, поділ поняття, множина, формула доповнення, поділ поняття за видотворною ознакою, дихотомія, класифікація, номінальне визначення, неявне визначення, контекстуальні і аксіоматичні визначення. Лекція. 1. Відношення між поняттями. У логіці всі поняття за змістом поділяються на порівнянні й непорівнянні. Порівнянні поняття – належать до одного предметного універсуму, тобто мають спільні родові ознаки. Наприклад, для понять “троянда” й “тигр” можна встановити спільну родову ознаку: “бути живим створінням”. Ці поняття є порівнянними. Непорівнянні поняття – не належать до одного предметного універсуму, тобто не мають спільних родових ознак. Наприклад, для таких пар понять, як “музика” і “потяг”, навряд чи можна знайти спільну родову ознаку. Ці поняття є непорівнянними. Певні відношення можна встановити лише між порівнянними поняттями, які, в свою чергу, поділяють на множину сумісних і множину несумісних понять. Сумісні поняття – поняття, обсяг яких збігається принаймі частково. Несумісні поняття – поняття, обсяг яких зовсім не збігається. Існує три типи відношень між поняттями, які є сумісними: § відношення тотожності; § відношення підпорядкування; § відношення перетину. I. Відношення тотожності. Тотожними називаються такі поняття, які хоча і мають різний зміст, але обсяги яких повністю співпадають. Схема відношення тотожності:
А – “вранішня зірка”; В – “вечірня зірка”.
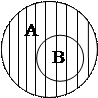
Ці поняття (А і В) є тотожними з огляду на те, що в їхніх обсягах узагальнюється один і той самий предмет – планета Венера, хоча узагальнення здійснюється на підставі різних ознак. II. Відношення підпорядкування. Відношення підпорядкування характеризує відношення між родовим поняттям і поняттям, що виражає (фіксує) один з видів цього роду. Тобто маються на увазі два поняття, обсяг одного з яких становить частину обсягу другого поняття. Схема відношення підпорядкування:
А – “ВУЗ”; В – “університет”.
За обсягом видове поняття В є вужчим, ніж родове поняття А, але за змістом видове поняття В включає в себе родове поняття А. ІІІ. Відношення перетину. Відношення перетину характеризує поняття, обсяги яких частково співпадають. Маються на увазі такі поняття, до обсягів яких включаються спільні елементи, однак, обсяг кожного з цих понять включає також предмети, що не являються елементами обсягу іншого поняття.
А – “свідок” В – “родич”
Існує три типи відношень між поняттями, що є несумісними: § відношення співпідпорядкування; § відношення протилежності; § відношення протиріччя. I. Відношення співпідпорядкування. Відношення співпідпорядкування характеризує відношення між поняттями, які є різними видами одного роду. У даному випадку обсягу родового поняття. Схема відношення співпідпорядкування:
II. Відношення протилежності. Відношення протилежності характеризує такі поняття, зміст яких відрізняється найвищою мірою, тобто: а) сума обсягів протилежних понять не вичерпує обсяг родового поняття; б) обсяги таких понять є двома крайніми видами в множині видів, які виділяються в межах певного роду на підставі деякої ознаки; в) одне з таких понять містить в собі ознаки, які не просто заперечують ознаки іншого поняття, але й замінюють їх на протилежні ознаки. Схема відношення протилежності:
В – “потворний” III. IV. Відношення протиріччя. Відношення протиріччя характеризує такі два поняття, які також є видами одного роду, але на відміну від відношення протилежності сума їх обсягів повністю вичерпує обсяг родового поняття, а зміст одного з них просто заперечує зміст іншого. Схема відношення протиріччя:
В – “незаконний”
Типи відношень між поняттями. (див. табл. №1 до лекції №3) 2. Операції над поняттями, їх классами. За певних умов, головною з яких є встановлення певного типу відношень між обсягами понять, над поняттями можна проводити операції додавання, множення і віднімання. Для того щоб ці операції були логічно коректні, необхідна певна формалізація понять і дій над ними, тобто представлення результатів у символічній та «геометричній» формах. Можна також проводити поділ, доповнення, класифікацію понять. Додавання понять. Це — операція над обсягами понять, сутність якої полягає в об’єднанні двох або кількох множин, що складають обсяги вихідних понять в одну множину. Головна вимога до результату додавання — не допустити «подвійного рахунку» елементів додавання, що збігаються (вони враховуються лише один раз), тобто сума повинна складатися лише з різних складових обсягу обох понять. Записується вона так: АÈВ. Об’єднувати можна класи, що знаходяться у будь-яких відношеннях один з одним:
(У першому випадку А - студенти, В – першокурсники, у другому випадку А – студенти, В – спортсмени). Додавання понять. (див. табл. №2 до лекції №3) Множення понять (перетину класів). Це — операція над поняттями, сутність якої полягає в утворенні нового поняття, обсягом якого є елементи, загальні для вихідних понять. Операція перетину класів (множення) полягає у відшуканні елементів, спільних для двох або кількох класів (множин). У нашому випадку це будуть студенти-спортсмени:
Операція перетину класів записується за допомогою знака множення: АÇВ. Множина, отримана у результаті множення називається, також, як і в математиці, добутком. При множенні несумісних понять, наприклад, «слідчі» та «адвокати», виходить пустий (нульовий) класс. Множення понять. (див. табл. №3 до лекції №3) Віднімання понять. Це — операція над обсягами понять, сутність якої полягає в тому, що утворюється нове поняття, елементи якого не входять до поняття, яке віднімається (див. табл. 4). Наприклад, якщо від класу «студенти» відняти клас «спортсмени», то залишаться студенти-неспортсмени. Операція віднімання класів дає клас, який виключає елементи класів, що віднімаються.
Віднімання понять. (див. табл. №4 до лекції №3) Операція доповнення обсягів понять (заперечення). Це — операція над поняттями, коли шляхом заперечення вихідного поняття А утворюють нове поняття А' (не-А), обсяг якого в сумі з обсягом поняття А складає цілісність, яка дорівнює одиниці (А + А' = 1) (див. рис. 1 до лекції №3). Формула доповнення: 1 – А = А'. Наприклад: 1 — вуз; А — гуманітарний вуз; А' = 1 – А (усі інші вузи, крім гуманітарних: технічні, економічні, військові та ін.). Поділ понять. Логічна операція, що розкриває обсяг поняття, називається поділом поняття. Поняття, обсяг якого розкривається, називається діленим поняттям. Ознака, за якою здійснюється поділ, називається основою поділу, а поняття, одержані в результаті поділу, членами поділу. Залежно від кількості членів поділу, розрізняють поділ двочленний, тричленний і багаточленний. Серед двочленного поділу виділяють дихотомію (від грец. dichotomia: dicha — два і tome — поділ, розтин, тобто поділ на дві частини), що являє собою поділ обсягу діленого поняття С на два суперечних поняття — А і не-А: швидкий — нешвидкий, збитковий — незбитковий і т. д. Існує також поділ поняття за видотворною ознакою (наприклад, науки поділяються на природничі, гуманітарні, технічні, економічні, медичні, юридичні та ін.). Особливим видом поділу є класифікація. Від звичайного поділу класифікація відрізняється тим, що в ній поділ здійснюється за істотною, корінною ознакою, а члени поділу займають постійне і чітко фіксоване місце. Прикладом класифікації може служити періодична система хімічних елементів Менделєєва.
|





 Схема відношення перетину:
Схема відношення перетину: А – “вищий учбовий заклад”
А – “вищий учбовий заклад”
 В – “ університет” С – “інститут”
В – “ університет” С – “інститут”

 А – “гарний”
А – “гарний”
 А – “законний”
А – “законний”