Рис. 1. Доповнення обсягів понять
| № п/п
| Назва закону
| Його формулювання
| Формула
| Її прочитання
| |
|
| Закон тотожності
| Кожне висловлювання тотожне саме собі
| А →А; А ↔;А
| «Якщо А, тоді А»; «А тоді і тільки тоді, коли А»
| |
|
| Закон несуперечності
| Жодне висловлювання не може бути істинним одночасно із своїм запереченням
| 
| «Неправильно, що А і не-А»
| |
|
| Закон виключеного третього
| 3 двох суперечних суджень одне неодмінно є істинним, не дано.
| 
| «А або не-А»
| |
|
| Закон достатньої підстави
| Будь-яка істинна думка повинна бути достатньо обгрунтованою
| Формального відображення не має
|
| |
|
| Закон подвійного речення:
|
|
|
| |
| 5.1
| Закон зняття подвійного заперечення
| Заперечення заперечення дає ствердження
| 
| Якщо неправильно, що не-А, тоді А»
| |
| 5.2
| Закон введення подвійного заперечення
| Із ствердження випливає його подвійне заперечення
| 
| «Якщо А, то хибно, ніби не-А»
| |
| 5.3
| Поний закон подвійного заперечення
| Подвійне заперечення тотожне ствердженню
| 
| «Хибно, що не-А тоді і тільки тоді, коли А»
| |
|
| Закони ідемпотентості:
|
|
|
| |
| 6.1
| Закон ідемпотентості для кон'юнкції
| Повтор висловлювання через сполучник кон'юнкції «і» є рівнозначним самому висловлюванню
| (А ^ А) ↔ А
| «А і А тоді і тільки тоді, коли А»
| |
| 6.2
| Закон ідемпотентості для диз'юнкції
| Повтор висловлювання через сполучник диз'юнкції «або» є рівнозначним самому висловлюванню
| (А v А) ↔ А
| А або А тоді і тільки тоді, коли А»
| |
|
| Закони комутативності:
|
|
|
| |
| 7.1
| Закон комутативності для кон'юнкції
| Можна міняти місцями висловлювання, зв'язані сполучником кон'юнкції «і»
| (АvВ)↔(ВvА)
| «А і В тоді і тільки тоді, коли В і А»
| |
| 7.2
| Закон комутативності для диз'юнкції
| Можна міняти місцями висловлювання, зв'язані сполучником диз'юнкції «або»
| (АvВ)↔(ВvА)
| «А або В тоді і тільки тоді, коли В або А»
| |
|
| Закони контрапозиції (простої і складної):
|
|
|
| |
| 8.1
| Перший закон простої контрапозиції
| Якщо з першого висловлювання випливає друге висловлювання, тоді із заперечення другого висловлювання випливає заперечення першого висловлювання
| (А→В)→( ) )
| «Коли відомо, що якщо А, то В, тоді якщо не-В. то не-А»
| |
| 8.2
| Другий закон простої контрапозиції
| Якщо із заперечення першого висловлювання випливає заперечення другого висловлювання, то з другого висловлювання випливає перше
| ( )→(В→А) )→(В→А)
| «Коли відомо, що якщо не-А, то не-В, тоді якщо В, то А»
| |
| 8.3
| Третій закон простої контрапозиції
| Якщо із першого висловлювання випливає заперечення другого висловлювання, то з другого висловлювання випливає заперечення першого висловлювання
| (А→  )→(В→ )→(В→  ) )
| «Коли відомо, що якщо А, то не-В, тоді якщо В, то не-А»
|
|
|
| 8.4
| Четвертий закон простої контрапозиції
| Якщо із заперечення першого висловлювання випливає друге висловлювання, то із заперечення другого висловлювання випливає перше висловлювання
| ( →В)→( →В)→( →А) →А)
| «Коли відомо, що якщо не-А, то В, тоді якщо не-В, то А»
|
| 8.5
| Перший закон складної контрапозиції
| 3 першого і другого висловлювань випливає третє висловлювання тоді і тільки тоді, коли 3 першого висловлювання і заперечення третього висловлювання випливає заперечення другого висловлювання
| 
| «Коли відомо, що з А і В випливає С, то тоді і тільки тоді з А і не -С випливає не -В»
|
| 8.6
| Другий закон складної контрапозиції
| 3 першого висловлювання випливає друге або третє висловлювання тоді і тільки тоді, коли із заперечення другого висловлювання випливає заперечення першого висловлювання або третє висловлювання
| 
| «Коли відомо, що якщо А, то В або С, то тоді і тільки тоді з не-В випливає не-А або С»
|
| 9.
| Закони асоціативності:
|
|
|
|
| 9.1
| Закон асоціативності для кон'юнкції
| Висловлювання, з'єднані логічним сполучником кон'юнкції «і», можна по-різному поєднувати за допомогою дужок
| ((А^В)^С)↔(А^(В^С))
| «(А і В) і С тоді і тільки тоді, коли А і (В і С)»
|
| 9.2
| Закон асоціативності для диз'юнкції
| Висловлювання, з'єднані логічним сполучником диз'юнкції «або», можна по-різному поєднувати за допомогою дужок
| ((А  В) В)  С)↔ (А С)↔ (А  (В (В  С)) С))
| «(А або В) або С тоді і тільки тоді, коли А або (В або С)»
|
|
| Закони дистрибутивності:
|
|
|
| |
| 10.1
| Закон дистрибутивності для кон'юнкції відносно диз'юнкції
| Дозволяється у формулах розподіляти кон'юнкцію відносно диз'юнкції
| ((А^(В^С)↔((А ^В)  (А^С)) (А^С))
| «А і (В або С), якщо і тільки якщо (А і В) або (А і С)»
| |
| 10.2
| Закон дистрибутивності для диз'юнкції відносно кон'юнкції
| Дозволяється у формулах розподіляти диз'юнкцію відносно кон'юнкції
| ((А  (В^С)↔ ((А (В^С)↔ ((А  В) ^ (А В) ^ (А  С)) С))
| «А або (В і С), якщо і тільки якщо (А або В) і (А або С)»
| |
|
| Закони де Моргана:
|
|
|
| |
| 11.1
| Перший закон де Моргана
| Заперечення кон'юнкції висловлювань еквівалентне диз'юнкції заперечень цих висловлювань
|  ↔( ↔(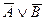 ) )
| «Хибно, що А і В тоді і тільки тоді, коли хибно, що А. або хибно, що В»
| |
| 11.2
| Другий закон де Моргана
| Заперечення диз'юнкції висловлювань еквівалентне кон'юнкції заперечень цих висловлювань
|  ↔( ↔( ) )
| «Хибно, що А або В тоді і тільки тоді, коли хибно, що А і хибно і ні"
| |
| | | | | | | | | | |














 Загально-стверджувальні
Загально-стверджувальні
 Частково-стверджувальні
Частково-стверджувальні
 Частково-заперечувальні
Частково-заперечувальні

 підпорядкування
підпорядкування




 )
)
 )→(В→А)
)→(В→А)
 )→(В→
)→(В→  )
)


 В)
В)  ↔(
↔(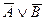 )
)
 ↔(
↔( )
)



