Устный опрос
а) Дайте определение матрицы. б) Какая матрица называется диагональной? в) Сформулируйте понятие единичной матрицы. г) Какие операции над матрицами вы знаете? д) Дайте понятие квадратной матрицы. е) Какие матрицы называются согласованными? ж) Дайте определения определителя, алгебраического дополнения и минора квадратной матрицы. з) Укажите формулы для вычисления определителей второго и третьего порядков. и) Сформулируйте основные свойства определителя. к) Перечислите способы вычисления определителя. л) Дайте определение ранга матрицы. м) Какая матрица называется канонической? н) Сформулируйте понятие эквивалентной матрицы. о) Какие элементарные преобразования матрицы вы знаете? п) Укажите необходимое и достаточное условие для существования обратной матрицы. р) Запишите формулу для вычисления обратной матрицы.
2. Разобрать примеры: Пример 1. Найти произведение матриц А= Решение. Имеем: матрица А размера 2´3, матрица В размера 3´3, тогда произведение АВ = С существует и элементы матрицы С равны с22 =3×2 + 1×0 + 0×5 = 6, с13 = 1×3 + 2×1 + 1×4 = 9, с23 = 3×3 + 1×1 + 0×4 = 10. AB = Пример 2. Дана матрица Решение. Вычислим алгебраические дополнения Аij=(-1)i+j Mij
Пример 3. Вычислить определитель Решение. 1. По правилу Саррюса Δ = 2*5*4+3*2*3+1*(-4)*1–1*5*3–3*(-4)*4–2*2*1 = 83 2.Разложим этот определитель по элементам первой строки:
Пример 4. Вычислить ранг матрицы.
Решение: вычислим минор 2-го порядка
Пример 5. Дана матрица Решение. 1 шаг. Вычислим 2 шаг. Вычислим алгебраические дополнения Аij=(-1)i+j Mij
3 шаг. Запишем А-1 4 шаг. Проверка правильности вычисления.
|
и В = 
.
, а произведение BA не существует.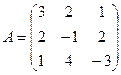
. Найти все её алгебраические дополнения.
, 
, 
, 
, 
, 
.
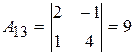
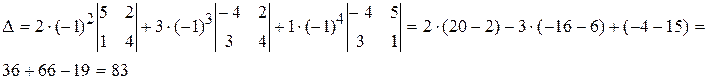
Так как существует ненулевой минор второго порядка, то r (A) = 2. Теперь вычислим все миноры 3-го порядка. Их всего четыре.
; 
; 
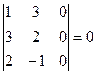. Т.к. все миноры 3-го порядка равны нулю, то r (A) = 2.
