Двумерные случайные величины.
Задание 5.1. Дискретная случайная величина
Найти закон распределения случайной величины Задание 5.2. Дискретная случайная величина
Найти закон распределения случайной величины Задание 5.3. Дискретная случайная величина
Найти закон распределения случайной величины Задание 5.4. Случайная величина Задание 5.5. Случайная величина Задание 5.6. Дискретные независимые случайные величины
Найти распределение случайной величины
Задание на дом.
Найти закон распределения случайной величины 2. Случайная величина 3. Случайная величина
Найти распределение случайной величины
Тема: Случайные функции. 1. Статистическое распределение выборки. Эмпирическая функция распределения, её свойства и график. Полигон и гистограмма частот. Задание 1.1. Выборка задана в виде распределения частот:
Найти распределение относительных частот. Задание 1.2. Найти функцию распределения по данному распределению выборки:
Задание 1.3. Найти функцию распределения по данному распределению выборки:
Задание 1.4. Построить полигон частот по данному распределению выборки:
Задание 1.5. Построить полигон относительных частот по данному распределению выборки:
Задание 1.6. Построить гистограмму частот по данному распределению выборки:
Задание 1.7. Построить гистограмму частот по данному распределению выборки:
Задание на дом.
Найти распределение относительных частот.
2. Статистические оценки параметров распределения. Критерии оценок. Генеральная средняя. Выборочная средняя. Групповая и общая средние. Задание 2.1. Из генеральной совокупности извлечена выборка объёма
Найти несмещённую оценку генеральной средней. Задание 2.2. Найти выборочную среднюю по данному распределению выборки:
Задание 2.3. Найти выборочную дисперсию по данному распределению выборки:
Задание 2.4. Найти выборочную дисперсию по данному распределению выборки:
Задание 2.5. Найти выборочную дисперсию по данному распределению выборки:
Задание на дом.
Найти несмещённую оценку генеральной средней.
Тема: Статистическое оценивание. 1. Дисперсии, их виды и способы вычисления. Точность оценки. Доверительные интервалы. Оценка истинного значения измеряемой величины. Оценка точности измерений. Задание 1.1. Случайная величина Задание 1.2. Найти методом моментов точеную оценку параметра Задание 1.3. Найти методом моментов по выборке
Задание на дом. 1. Найти методом моментов точечную оценку параметра 2. Найти методом моментов точечную оценку параметра
2. Функциональная, статистическая и корреляционная зависимости. Условные средние. Выборочные уравнения регрессии. Корреляционная таблица. Выборочный коэффициент корреляции. Выборочное корреляционное отношение. Простейшие случаи криволинейной корреляции. Задание 2.1. Найти выборочное уравнение прямой линии регрессии
Задание 2.2. Найти выборочное уравнение регрессии
Задание на дом.
Два товароведа расположили девять мотков шерсти в порядке убывания толщины нити. В итоге были получены две последовательности рангов:
Найти коэффициент ранговой корреляции Спирмена между рангами
Статистическая гипотеза. Нулевая и конкурирующая, простая и сложная гипотезы. Ошибки первого и второго рода. Сравнения дисперсий, нормальных совокупностей, генеральных совокупностей, нормальных биномиальных распределений. Задание 3.1. По двум независимым выборкам, объёмы которых Задание 3.2. По двум независимым выборкам, объёмы которых Задание 3.3. Из нормальной генеральной совокупности извлечена выборка объёма
Задание на дом. 1. По двум независимым выборкам, объёмы которых 2. Из нормальной генеральной совокупности извлечена выборка объёма Литература
|

 задана законом распределения:
задана законом распределения: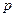
 .
. .
.


 .
. . Найти плотность распределения
. Найти плотность распределения  случайной величины
случайной величины  в интервале
в интервале  ; вне этого интервала
; вне этого интервала  . Найти математическое ожидание функции
. Найти математическое ожидание функции  .
. заданы распределениями:
заданы распределениями: .
. .
. .
. .
.




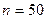 :
: :
:  , где
, где  - число испытаний, проведённых в одном опыте,
- число испытаний, проведённых в одном опыте, 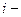 м опыте. Найти методом моментов по выборке
м опыте. Найти методом моментов по выборке  точечную оценку параметра
точечную оценку параметра  , определяющего данное распределение.
, определяющего данное распределение. , где
, где  точечную оценку параметра
точечную оценку параметра  .
. , где
, где 


 по данным, приведённым в следующей корреляционной таблице:
по данным, приведённым в следующей корреляционной таблице:
 и
и  , извлечённым из нормальных генеральных совокупностей
, извлечённым из нормальных генеральных совокупностей  и
и  . При уровне значимости
. При уровне значимости  , проверить нулевую гипотезу
, проверить нулевую гипотезу  :
: 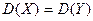 о равенстве генеральных дисперсий при конкурирующей гипотезе
о равенстве генеральных дисперсий при конкурирующей гипотезе  :
:  .
. и
и  , извлечённым из нормальных генеральных совокупностей
, извлечённым из нормальных генеральных совокупностей  и
и  . При уровне значимости
. При уровне значимости  .
. и по ней найдена исправленная выборочная дисперсия
и по ней найдена исправленная выборочная дисперсия  . Требуется при уровне значимости
. Требуется при уровне значимости 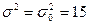 , приняв в качестве конкурирующей гипотезы
, приняв в качестве конкурирующей гипотезы  .
. , извлечённым из нормальных генеральных совокупностей
, извлечённым из нормальных генеральных совокупностей  и
и 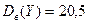 . При уровне значимости
. При уровне значимости  и по ней найдена исправленная выборочная дисперсия
и по ней найдена исправленная выборочная дисперсия  . Требуется при уровне значимости
. Требуется при уровне значимости  проверить нулевую гипотезу
проверить нулевую гипотезу  , приняв в качестве конкурирующей гипотезы
, приняв в качестве конкурирующей гипотезы  .
.


