ИДЗ № 1
ЗАДАНИЯ 1 – 20 Даны матрицы А, В, С, D. Найти: а) P=(2А–3В)C б) ранг матрицы D. 1. 2. 3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
ЗАДАНИЯ 21 – 45 Для данного определителя
21. i=4, j=1. i=3, j=3.
23. i=4, j=1. i=1, j=3.
25. i=2, j=4. i=1, j=2.
27. i=2, j=3. i=3, j=1.
29. i=4, j=3. i=4, j=2.
31. i=4, j=1. i=3, j=3.
33. i=4, j=1. i=1, j=3.
35. i=2, j=4. i=1, j=2.
37. i=2, j=3. i=3, j=1.
39. i=4, j=3. i=4, j=2.
41. i=2, j=4. i=1, j=2.
43. i=2, j=3. i=3, j=1.
45. i=4, j=3.
ЗАДАНИЯ 46 – 65 Найти общую стоимость сырья, планируемую для производства продукции двух видов P1 и P2, если план выпуска продукции задан матрицей P=(p1, p2); нормы расхода сырья трёх типов S1, S2, S3 на единицу продукции P i заданы матрицей S и известна стоимость (у.е.) единицы сырья каждого вида – матрица С. 46 48 50 52 54 56 58 60 62 64
ЗАДАНИЯ 66-90 Проверить совместность системы уравнений и в случае совместности решить ее: 1) по формуле Крамера; 2) с помощью обратной матрицы (матричным методом); 3) методом Гаусса.
66.
68
70
72
74
76
78
80
82
84
86
88
90 ЗАДАНИЯ 91-110 Исследовать системы на совместность. Найти общее решение в случае совместности.
91
93 95
97
99
101
103
105
107
109 ИДЗ № 2
|



 ;
; 


 ;
; 



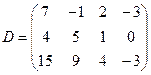





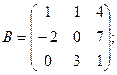




 ;
; 
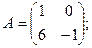





 ;
; 



























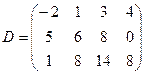







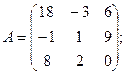











 найти миноры и алгебраический дополнения элементов
найти миноры и алгебраический дополнения элементов  . Вычислить определитель: 1) разложив его по элементам i-той строки; 2) разложив его по элементам j-го столбца.
. Вычислить определитель: 1) разложив его по элементам i-той строки; 2) разложив его по элементам j-го столбца. 22.
22. 
 24.
24. 
 26.
26. 
 28.
28. 
 30.
30. 
 32.
32. 
 34.
34. 
 36.
36. 
 38.
38. 
 40.
40. 
 42.
42. 
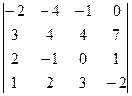 44.
44. 

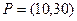 ;
;  ;
;  . 47
. 47  ;
;  ;
;  .
. ;
;  ;
;  . 49
. 49  ;
;  .
. ;
;  ;
;  . 51
. 51  ;
;  ;
;  ;
;  ;
;  . 53
. 53  ;
;  ;
;  ;
;  . 55
. 55  ;
;  ;
;  .
. ;
;  . 57
. 57  ;
;  .
. ;
;  . 59
. 59  ;
;  .
. ;
;  ;
;  . 61
. 61  ;
;  ;
;  . 63
. 63  ;
;  ;
;  .
. ;
;  . 65
. 65  ;
;  67
67 
 69
69 
 71
71 
 73
73 
 75
75 
 77
77 
 79
79 
 81
81 
 83
83  85
85  87
87 
 92
92 
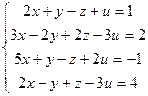 94
94 
 96
96 
 98
98 
 100
100 
 102
102 
 104
104 
 106
106 
 108
108 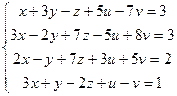
 110
110 



