Устный опрос. а) Производная функции (определение).
а) Производная функции (определение). б) Общее правило нахождения производной. в) Правила дифференцирования суммы, произведения, частного двух функций: г) Таблица производных основных элементарных функций. д) Сложная функция (определение). е) Правило дифференцирования сложной функции. ж) Примечания к правилу дифференцирования функций. з) Понятие производной. и) Дифференциал функции (определение). к)
Решение упражнений Используя определение производной, найти производные функций в точке х 2.1. [у=sinx; у= 2.2. [у= 2х; у=5х3; у= соs 2х; у= Используя определение производной, найти f′(0), если 2.1. 2.2. а) Продиференцировать следующие функции: [ у=х5; у = х; у = 2.1. а) у=х/2+х3/3+2/х–6/х2; б) у=(х2-х+3)(х3+2х2+4); в) у = х/(х2-1); г) у = х2cosx/(1-tgx)]
2.2. а) у=(х3-х+7)(х4+х2-2); б) у=(1+ в) е) Дифференцирование более сложных функций: 2.1. а) у= cos д) у=sin4х2; е) у = ctg 2.2. а) у = lnsinx; б) у =(arccosx)3; в) у = cos3x; г) у = ln3x. д) у=sin2 5х; е) у = Используя понятие дифференциала, вычислить приближенно: . а) 1.0050,5; б) 1,035. В) 1,021/3.
Литература: 1. Сборник задач по высшей математике для экономистов [Текст]: учебное пособие/ Под ред. В. И. Ермакова.- 2-е изд., испр.- М.: Инфра - М, 2010.- 575 c. 2. Баврин, И.И. Математика: учебник для студентов учреждений высшего пед. и психол. пед. проф. образования / И.И. Баврин – 10-е изд. стер.. –М.: Издательский центр «Академия», 2013г.- 624 с. Тема: «Интегрирование» План:
|

 ;
;  ;
;  ;(
;(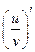 ).
).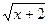 в точке х и в точке х0=2]
в точке х и в точке х0=2]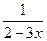 в точке х]
в точке х]
 б)
б) 
 ](Устно)
](Устно) )(1+2
)(1+2  ; г) у=tgx+arccosx; д)
; г) у=tgx+arccosx; д)  ;
; ; ж)
; ж)  ; з) у=ех·tgx; и) у=6х
; з) у=ех·tgx; и) у=6х ; в) у= еsinx; г) у= arcsin ех.
; в) у= еsinx; г) у= arcsin ех. ; ж) у = е
; ж) у = е 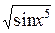
 .
.


