Характеристика двух систем управления запасами
Уровень запаса определяется как остаток материалов перед предыдущей поставкой, плюс количество полученных материалов, минус израсходованное количество. Определение оптимальной величины заказа производится при следующих допущениях: 1) потребность в материале постоянна и равномерно распределена по всему периоду использования материалов; 2) время выполнения заказа постоянно; 3) цена единицы материалов постоянна; 4) затраты на размещение заказа постоянны; 5) для закупок любых количеств материала имеются необходимые ресурсы и исключается возможность невыполнения заказа. Затраты на создание запасов можно выразить следующим уравнением:
где Z— суммарные годовые затраты; Q — количество материала, которое необходимо заказать; С — цена единицы закупаемого материала; N— затраты на размещение заказа В — затраты на хранение запаса; На рис.38 показано графическое изображение зависимости (3).
Qопт Рис.38 Графическое изображение зависимости (3) Здесь Qопт — оптимальный уровень заказа.
Модель управления запасами простейшего типа (однопродуктовая статическая модель) характеризуется постоянным во времени спросом, мгновенным пополнением запаса и отсутствием дефицита. Интенсивность спроса в единицу времени β;, наивысший запас – в момент поставки размером У (рис.39). Он полностью расходуется через промежуток времени, равный tо =У/β;(4)
Запаса
Рис.39 Однопродуктовая статическая модель Чем меньше Y, тем чаще нужно размещать заказ, с увеличением размера заказов заказы размещаются реже. Суммарные затраты в единицу времени z(y) можно представить в виде: z(y) = Здесь N – затраты на оформление (размещение) заказа; y – размер заказа; β – интенсивность спроса в единицу времени
b(
Оптимальный размер заказа определяется из зависимости
Откуда оптимальное значение заказа у * определяется зависимостью
Выражение (7) называется формулой экономичного размера заказа Уилсона. Оптимальная стратегия модели предусматривает заказ у* единиц продукции через каждые tоп=y*/ β; единиц времени. Оптимальные затраты:
Чтобы не возникал дефицит, заказ на склад должен подаваться в тот момент, когда в запасе еще имеется некоторое количество товаров, достаточное для удовлетворения ожидаемого спроса до получения нового заказа. Это количество запаса называется точкой заказа (рис.40).
tз tз Время Рис.40 Определение точки заказа Пример решения задачи Ежедневный спрос на некоторый товар составляет 150 ед. Затраты на размещение заказа и равны 120 у.е. Ежедневные затраты на хранение единицы запаса составляют 0,03у.е., срок выполнения заказа равен 10 дням. Определить экономичный размер партии и точку заказа.
|

 Z= (QC+N +В) max (3),
Z= (QC+N +В) max (3),
 Z
Z Суммарные затраты
Суммарные затраты
 затраты на хранение запаса
затраты на хранение запаса
 затраты на материалы
затраты на материалы
 затраты на размещение заказа
затраты на размещение заказа Q
Q


 Средний уровень
Средний уровень


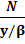 +b (
+b (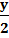 ) (5)
) (5)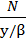 – затраты на оформлениезаказа в единицу времени;
– затраты на оформлениезаказа в единицу времени; ) – затраты на хранение запаса в единицу времени.
) – затраты на хранение запаса в единицу времени.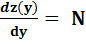 β/y2 + b/2 (6)
β/y2 + b/2 (6) у* = √2Nβ/b (7)
у* = √2Nβ/b (7) z (у*) =
z (у*) = 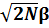 b (8)
b (8)






