Практическая методика статистической обработки результатов измерений
С целью унификации записей обработка данных производится в форме, представленной в табл. 1. Таблица 1
Примечание. […] – единица измерения. Для заполнения таблицы нужно произвести следующие действия. 1. Записать в табл. 1 данные, полученные Вами при выполнении измерений или расчётов. 2. Найти среднее значение измеренной величины по формуле (2), записать в соответствующую ячейку таблицы с запасной значащей цифрой. 3. Вычислить отклонения от среднего (формула (3)). Отрицательные отклонения записать в столбик под знаком «–», положительные – под знаком «+». 4. Вычислить сумму положительных и отрицательных отклонений. При правильно найденном среднем значении эти суммы должны быть одинаковыми. (Из-за округления среднего значения могут быть незначительные расхождения между суммами.) 5. Найти среднюю абсолютную погрешность, сложив суммы положительных и отрицательных отклонений и поделив на число измерений (а не на 2!). 6. Записать результат измерений (см. формулу (1)) в виде
округлив áD Х ñ до одной значащей цифры (допускается до двух значащих цифр, если первая значащая 1 или 2). Среднее значение á Х ñ также нужно округлить до того разряда, на котором заканчивается средняя абсолютная погрешность (см. примеры в п. 8 предыдущего параграфа). 7. Найти относительную погрешность измерений по формуле (6), округлить до 1–2 значащих цифр и записать в последнюю строку таблицы. В качестве примера ниже приведена таблица обработки результатов измерения штангенциркулем (приборная погрешность 0,1 мм) некоторого размера L.
Таблица 2
Обратите внимание! Значения Li записаны в таблице с той точностью, которую даёт прибор – все числа с тремя значащими цифрами. Среднее значение этой величины записано с запасной цифрой. Результат же измерений записан без этой запасной цифры. Абсолютная погрешность округлена до одной значащей цифры, разряд которой – десятые доли миллиметра, поэтому и среднее значение округлено до десятых.
|

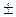 áD Х ñ) […]
áD Х ñ) […]
 мм
мм