Гироскопическая вертикаль с маятниковой коррекцией
Одним из наиболее распространенных авиационных гироскопических приборов является гироскопическая вертикаль (гирогоризонт) с маятниковой коррекцией. Чувствительным элементом датчика сигнала коррекции гировертикали служит маятник, который при отсутствии ускорений устанавливается по направлению силы тяжести, т.е. вертикально. При ускорениях, возникающих в полете, маятник отклоняется от вертикали, совершая колебательные движения. Гироскоп, обладающий малой чувствительностью к внешним возмущениям, сглаживает (фильтрует) колебания маятника. В результате направление определяется с большей точностью, чем просто маятником. На рис. 3.2 показана принципиальная схема коррекции положения гироскопа относительно оси внутренней рамки подвеса. Позиционный сигнал для коррекции образуется при отклонении главной оси гироскопа от маятника, т.е. при угле Под действием корректирующего момента гироскоп, подчиняясь правилу прецессии, начинает прецессировать так, что вектор кинетического момента К стремится к вектору корректирующего момента С помощью маятника задается позиционный сигнал, указывающий положение, которое должна занять главная ось гироскопа. В связи с этим подобную систему коррекции называют позиционной.
Рис. 3.2. Схема гировертикали с маятниковой коррекцией.
Закон изменения корректирующего момента от угла Линейная характеристика (рис. 3.3,а). Корректирующий момент
Рис. 3.3. Характеристики системы коррекции гироскопа: а - график линейной характеристики; б- график релейной характеристики; в - график смешанной характеристики
Релейная характеристика (рис. 3.3,6). Модуль корректирующего момента
График смешанной характеристики с ограниченной зоной линейности показан на рис. 3.3,в. Важной характеристикой гироскопа с коррекцией является отношение величины корректирующего момента Ориентируем систему отсчета В рассматриваемом случае момент I. Корректирующий момент
Рис. 3.4. Отклонения маятника от вертикали Проекции вектора корректирующего момента на оси х и у составят
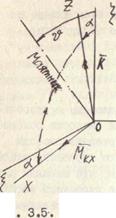
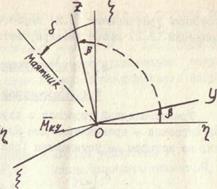
Рис. 3.5. Отклонения маятника и главной оси гироскопа в различных плоскостях
2. Момент Момент Проекции момента Проекции
в уравнения (I.I5). Выполнив Подставим значения
получим уравнения относительного движения гировертикали с линией
где
Как видим, относительное движение гировертикали с линейной характеристикой коррекции приближенно описывается неоднородными линейными уравнениями (3.2) первого порядка. При этом каждое из уравнений (3.2) может интегрироваться независимо от другого.
|

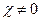 . Через усилитель У этот сигнал воздействует на мотор коррекции
. Через усилитель У этот сигнал воздействует на мотор коррекции  , создающий корректирующий момент
, создающий корректирующий момент 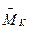 относительно оси внешней рамки подвеса гироскопа.
относительно оси внешней рамки подвеса гироскопа.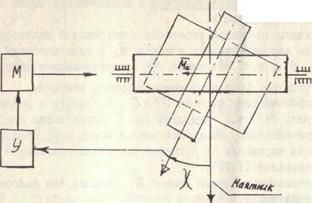
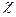 является одной из основных характеристик системы коррекции гироскопа. Рассмотрим эти характеристики.
является одной из основных характеристик системы коррекции гироскопа. Рассмотрим эти характеристики. , где k - коэффициент усиления.
, где k - коэффициент усиления.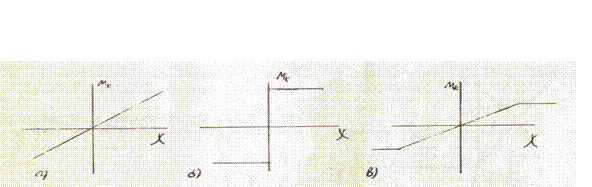
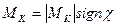
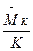 , определяющее скорость прецессии гироскопа, вызванной корректирующим моментом.
, определяющее скорость прецессии гироскопа, вызванной корректирующим моментом.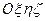 , связанную с Землей, как показано на рис. 2.3, т.е. направим ось
, связанную с Землей, как показано на рис. 2.3, т.е. направим ось 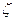 вертикально вверх а ось
вертикально вверх а ось  подобно тому, как ранее определяли отклонение главной оси гироскопа относительно того же направления (см. рис. 1.6). При малых отклонениях приближенно можно принять, что углы
подобно тому, как ранее определяли отклонение главной оси гироскопа относительно того же направления (см. рис. 1.6). При малых отклонениях приближенно можно принять, что углы 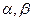 , определяющими отклонение главной оси гироскопа (рис. 3.5).
, определяющими отклонение главной оси гироскопа (рис. 3.5).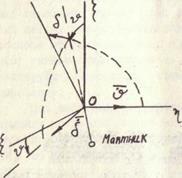
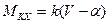 ,
, 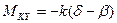 .
.
 , вызванный дебалансом гироскопа. Проекции момента
, вызванный дебалансом гироскопа. Проекции момента 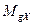 и
и 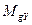 .
.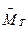 , вызванный трением в опорах подвеса гироскопа.
, вызванный трением в опорах подвеса гироскопа.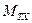 и
и 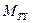
 и
и 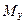 суммарного момента внешних сил в данном случае составят
суммарного момента внешних сил в данном случае составят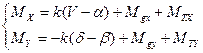 (3.1)
(3.1)
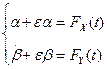 (3.2)
(3.2)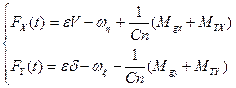 (3.3)
(3.3)


