Изучим относительное движение главной оси гироскопа. Для этого рассмотрим движение одной ее точки α, удаленной на единицу длины от точки закрепления гироскопа в положительном направлении оси z. Такую точку назовем вершиной гироскопа, или апексом.
Вершина гироскопа движется по сфере единичного радиуса с центром в точке закрепления 0. Положение вершины гироскопа на этой сфере определяется двумя углами.
Система отсчета 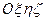 (рис. 1.5), относительно которой рассматривается движение оси гироскопа, связана со сферой. В начальном положении трехгранник
(рис. 1.5), относительно которой рассматривается движение оси гироскопа, связана со сферой. В начальном положении трехгранник  совпадает с трехгранником
совпадает с трехгранником 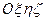 .
.
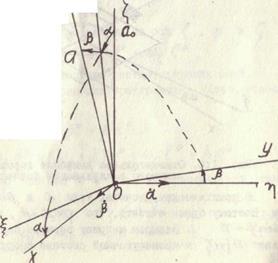
Рис. 1.5. Относительное движение вершины гироскопа
Повернем трехгранник  вокруг оси
вокруг оси 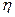 на угол
на угол  с угловой скоростью
с угловой скоростью 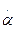 . Ось
. Ось 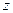 займет положение
займет положение  , а ось
, а ось 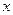 -положение, показанное на рис. 1.5.
-положение, показанное на рис. 1.5.
Затем повернем трехгранник 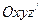 вокруг оси х на угол
вокруг оси х на угол  с угловой скоростью
с угловой скоростью 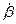 . Ось z' переместится при этом в положение z, а ось y - в положение, показанное на рис. 1.5. Углы
. Ось z' переместится при этом в положение z, а ось y - в положение, показанное на рис. 1.5. Углы  и
и  определят положение вершины гироскопа на сфере.
определят положение вершины гироскопа на сфере.
Условимся считать приращения углов  и
и  положительными, если векторы угловых скоростей
положительными, если векторы угловых скоростей 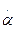 и
и 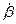 совпадают с положительными направлениями осей
совпадают с положительными направлениями осей  .
.
Система отсчета 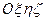 связана с основанием гироскопа, закрепленного в кардановом подвесе. Ось
связана с основанием гироскопа, закрепленного в кардановом подвесе. Ось  направим по оси внешней рамки подвеса гироскопа, а ось x системы отсчета
направим по оси внешней рамки подвеса гироскопа, а ось x системы отсчета  - по оси внутренней рамки подвеса (рис. 1.6). Тогда угол
- по оси внутренней рамки подвеса (рис. 1.6). Тогда угол  , определит поворот внешней рамки гироскопа относительно основания, а угол
, определит поворот внешней рамки гироскопа относительно основания, а угол  - поворот внутренней рамки подвеса гироскопа относительно внешней.
- поворот внутренней рамки подвеса гироскопа относительно внешней.
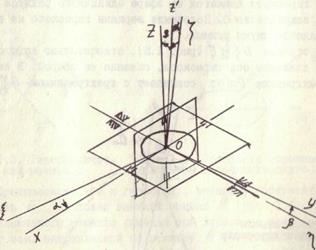
Рис. 1.6. Относительное движение гироскопа, закрепленного в кардановом подвесе
В практических расчетах углы  обычно остаются малыми. Поэтому будем считать, что
обычно остаются малыми. Поэтому будем считать, что 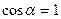 ,
, 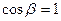 ,
,  ,
,  . Запишем матрицу первого перехода от системы координат
. Запишем матрицу первого перехода от системы координат  к промежуточной системе координат
к промежуточной системе координат  :
:
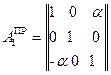
Матрица второго перехода от промежуточной системы  к системе Охуz
к системе Охуz
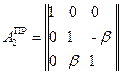
Матрица перехода от первой системы координат 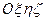 ко второй
ко второй
системе координат  равна произведению матриц первого и
равна произведению матриц первого и
второго переходов:
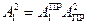
Пренебрегая произведением малых углов, найдем
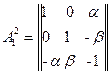 (1.12)
(1.12)
Вектор угловой скорости вращения трехгранника  можно представить как сумму двух векторов - вектора угловой скорости
можно представить как сумму двух векторов - вектора угловой скорости  вращения системы отсчета
вращения системы отсчета 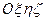 и вектора угловой скорости
и вектора угловой скорости  , с которой трехгранник
, с которой трехгранник  , вращается относительно системы отсчета
, вращается относительно системы отсчета 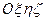 :
:
 .
.
Вектор  можно задать его проекциями на оси
можно задать его проекциями на оси  :
:
 ,
,
где  - единичные векторы соответствующих осей.
- единичные векторы соответствующих осей.
Вектор угловой скорости вращения трехгранника  относительно системы отсчета
относительно системы отсчета 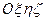
 .
.
Следовательно,
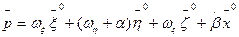
Спроектируем вектор 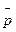 на оси
на оси  , использовав при этом матрицу (I.I2). Получим
, использовав при этом матрицу (I.I2). Получим
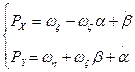 (1.13)
(1.13)
Угловая скорость  обычно невелика. Вторые члены правых частей уравнений (I.I3), представляющие собой произведения малых величин, можно не учитывать.
обычно невелика. Вторые члены правых частей уравнений (I.I3), представляющие собой произведения малых величин, можно не учитывать.
Подставим значения  в два первых уравнения (1.7), отбросив в правых частях уравнений (1.13) малые вторые члены.
в два первых уравнения (1.7), отбросив в правых частях уравнений (1.13) малые вторые члены.
Найдем
 (1.14)
(1.14)
Подставим далее значения  в систему уравнений (1.9) При этом же допущении получим
в систему уравнений (1.9) При этом же допущении получим
 (1.15)
(1.15)
Уравнения (1.14) и (1.15) - приближенные и описывают движение оси гироскопа относительно подвижной (вращающейся) системы отсчета 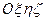 с различной степенью точности.
с различной степенью точности.
Усеченные уравнения (1.15) описывают только прецессию гироскопа. Полные уравнения (1.14) учитывают дополнительное движение главной оси гироскопа относительно его кинетической оси.

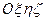 (рис. 1.5), относительно которой рассматривается движение оси гироскопа, связана со сферой. В начальном положении трехгранник
(рис. 1.5), относительно которой рассматривается движение оси гироскопа, связана со сферой. В начальном положении трехгранник  совпадает с трехгранником
совпадает с трехгранником 
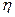 на угол
на угол  с угловой скоростью
с угловой скоростью 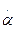 . Ось
. Ось 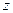 займет положение
займет положение  , а ось
, а ось 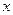 -положение, показанное на рис. 1.5.
-положение, показанное на рис. 1.5. вокруг оси х на угол
вокруг оси х на угол  с угловой скоростью
с угловой скоростью 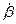 . Ось z' переместится при этом в положение z, а ось y - в положение, показанное на рис. 1.5. Углы
. Ось z' переместится при этом в положение z, а ось y - в положение, показанное на рис. 1.5. Углы  .
. направим по оси внешней рамки подвеса гироскопа, а ось x системы отсчета
направим по оси внешней рамки подвеса гироскопа, а ось x системы отсчета 
 обычно остаются малыми. Поэтому будем считать, что
обычно остаются малыми. Поэтому будем считать, что 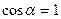 ,
, 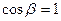 ,
,  ,
,  . Запишем матрицу первого перехода от системы координат
. Запишем матрицу первого перехода от системы координат  :
: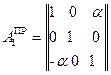
 к системе Охуz
к системе Охуz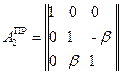
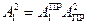
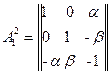 (1.12)
(1.12) вращения системы отсчета
вращения системы отсчета  , с которой трехгранник
, с которой трехгранник  .
. :
: ,
, - единичные векторы соответствующих осей.
- единичные векторы соответствующих осей. .
.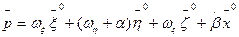
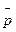 на оси
на оси  , использовав при этом матрицу (I.I2). Получим
, использовав при этом матрицу (I.I2). Получим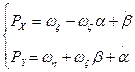 (1.13)
(1.13) обычно невелика. Вторые члены правых частей уравнений (I.I3), представляющие собой произведения малых величин, можно не учитывать.
обычно невелика. Вторые члены правых частей уравнений (I.I3), представляющие собой произведения малых величин, можно не учитывать. в два первых уравнения (1.7), отбросив в правых частях уравнений (1.13) малые вторые члены.
в два первых уравнения (1.7), отбросив в правых частях уравнений (1.13) малые вторые члены. (1.14)
(1.14) (1.15)
(1.15)


