Правило прецессии
К гироскопу, кинетический момент которого равен
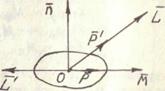
Рис. 1.2 Правило прецессии Модуль угловой скорости вращения
Где Направление вращения таково, что вектор Правило прецессии формулируется следующим образом: под действием внешнего момента Ось, совпадающую с направлением вектора кинетического момента, называют кинетической осью. Кинетическая ось не совпадает с главной осью гироскопа. Поскольку угол между направлениями кинетической и главной осей весьма мал, практически можно считать, что кинетическая ось гироскопа совпадает с его главной осью. Главная ось гироскопа, следуя за кинетической осью, в то же время совершает около нее быстрые колебания. Это дополнительное движение главной оси гироскопа около кинетической оси выражается в виде мелкого дрожания, незаметного для глаза. Кинетический момент гироскопа
где Отсюда видно, что кинетический момент гироскопа можно увеличить двумя путями: увеличением момента инерции гироскопа относительно главной оси и увеличением собственной угловой скорости гироскопа. В малогабаритных авиационных гироскопах предпочтение отдается второму пути. Скалярные уравнения движения гироскопа. Запишем скалярные уравнения движения гироскопа в подвижной прямоугольной системе координат Охуz, начало которой находится в центре приведения моментов 0. Проектируя векторное уравнение (1.3) на оси координат
Уравнения (1.5) принимают удобный для исследования вид в случае, если центр приведения 0 и начало координат находятся в точке закрепления гироскопа, а ось z направлена по его главной оси. Оси Проекции вектора кинетического момента
где A, В, С - осевые моменты инерции гироскопа; Абсолютная угловая скорость гироскопа
где р - угловая скорость системы отсчета; n - вектор составной (относительной) угловой скорости гироскопа, направленный по оси z. Поэтому
Заменим в уравнениях (1.5) проекции вектора
Практически, собственная угловая скорость гироскопа n, которая сообщается ему относительно главной оси, значительно превосходит переносную угловую скорость р, с которой вращается система отсчета
Поэтому в левой части двух первых уравнений (1.6) вторые члены будут малы по сравнению с последними членами. Отбрасывая эти малые члены, получим систему уравнений
Вектор кинетического момента направлен по главной оси гироскопа. При таком допущении и выбранном направлении координатных осей будем иметь
и, следовательно В рассматриваемом случае уравнения (1.5) упрощаются и принимают вид
Собственная угловая скорость гироскопа n значительно превосходит переносную угловую скорость р, с которой вращается система отсчета
В системах уравнений (1.6), (1.7) и (1.9) два первых уравнения описывают движение главной оси гироскопа. Последнее уравнение является уравнением вращения гироскопа относительно главной оси.
Гироскопический момент. Гироскопический эффект. Вектор, равный по величине и противоположно направленный вектору внешнего момента М, представляет момент инерционного сопротивления, которое оказывает тело, в том числе и гироскоп, внешним воздействием. Выделим в левой части уравнений (1.6) члены, содержащие угловую скорость гироскопа n. Эти члены, взятые с противоположным знаком, представляют собой инерционное сопротивление, специфичное для гироскопа. Обозначая I момент этого инерционного сопротивления, можем записать
Момент где i и j - орты осей x и у, называют гироскопическим моментом. Нетрудно убедиться, что гироскопический момент
Для этого достаточно разложить вектор_ Вектор гироскопического момента
Рис. 1.3. Гироскопический момент
Рис. 1.4. Прецессия гироскопа под действием гироскопического момента
Предположим, что к гироскопу, имеющему собственную угловую скорость Моменты Моменты Внешнее проявление гироскопического момента называют гироскопическим эффектом. Прецессия гироскопа является одним из примеров гироскопического эффекта.
|

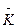 , приложен внешний момент
, приложен внешний момент 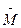 (рис. 1.2), причем угол между векторами
(рис. 1.2), причем угол между векторами  . Вектор
. Вектор 

 - составляющая вектора внешнего момента, нормальная к вектору кинетического момента
- составляющая вектора внешнего момента, нормальная к вектору кинетического момента 
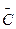 - момент инерции гироскопа относительно главной оси; n -собственная угловая скорость, сообщенная гироскопу относительно той же оси.
- момент инерции гироскопа относительно главной оси; n -собственная угловая скорость, сообщенная гироскопу относительно той же оси.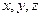 получим уравнения Эйлера
получим уравнения Эйлера (1.5)
(1.5) могут быть направлены произвольно. В этом случае оси,
могут быть направлены произвольно. В этом случае оси, 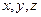 совпадают с главными осями инерции гироскопа.
совпадают с главными осями инерции гироскопа.
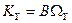
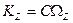 ,
, - абсолютная угловая скорость гироскопа.
- абсолютная угловая скорость гироскопа.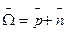 ,
,
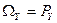
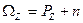 .
. (1.6)
(1.6) . Кроме того,
. Кроме того,
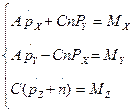 (1.7)
(1.7)

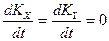 .
.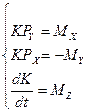 (1.8)
(1.8) . Подставив значение К в приближенные уравнения (1.8), получим
. Подставив значение К в приближенные уравнения (1.8), получим (1.9)
(1.9)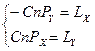
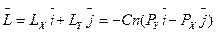

 по координатным осям.
по координатным осям. . (1.11)
. (1.11)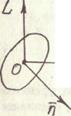
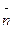 , приложен внешний момент
, приложен внешний момент 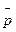 . Но при вращении оси гироскопа возникает гироскопический момент
. Но при вращении оси гироскопа возникает гироскопический момент 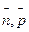 . Возникший гироскопический момент в свою очередь вызывает вращение главной оси гироскопа с некоторой угловой скоростью
. Возникший гироскопический момент в свою очередь вызывает вращение главной оси гироскопа с некоторой угловой скоростью 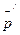 , направленной по вектору
, направленной по вектору 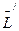 , направленный в сторону, противоположную внешнему моменту
, направленный в сторону, противоположную внешнему моменту 


