Применение свободного гироскопа в курсовых системах
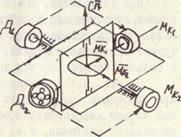
Курсовые системы предназначаются для определения курса ЛА. Если главную ось свободного гироскопа установить горизонтально в плоскости меридиана или под некоторым известным углом по отношению к этой плоскости, то можно считать, что угол между главной осью гироскопа и плоскостью меридиана в течение некоторого времени остается постоянным. Это дает возможность использовать свободный гироскоп в курсовых системах как начало отсчета при измерении курса. Гироскоп, входящий в курсовую систему, называют курсовым гироскопом. С помощью свободного курсового гироскопа можно определить только изменение курса, но не абсолютное его значение. Поэтому свободный курсовой гироскоп называют также гирополуком-пасом. Ось внешней рамки подвеса курсового гироскопа при горизонтальном полете ЛА располагается вертикально (рис. 2.10).
Рис. 2.10. Установка курсового гироскопа на ЛА
Девиации курсового гироскопа возникают по тем же причинам, что и девиации гировертикали. Девиация курсового гироскопа, вызванная вращением Земли. Пусть гироскоп установлен на неподвижном относительно Земли основании. Закрепленная точка гироскопа находится в точке 0 (рис. 2.II). Широта места точки 0 равна
Рис. 2.11. Девиация курсового гироскопа, вызванная вращением Земли
Возьмем систему отсчета Система отсчета
Подставим эти значения в уравнения (1.15) относительного движения гироскопа. Для свободного гироскопа при отсутствии трения в подвесе, которым можно пренебречь,
Интегрируя уравнения (2.12) по времени при нулевых начальных условиях, т.е. при
Уравнения (2.12) и (2.13) определяют девиацию курсового гироскопа вследствие вращения Земли за небольшой промежуток времени t, в пределах малых значений углов Интенсивность девиации курсового гироскопа и ее направление зависят от широты Изменение угла Скоростная девиация. Спроектируем на оси
Подставим
Рис. 2.12. Девиация курсового гироскопа Рис. 2.13. Скоростная девиация курсового гироскопа Уравнения (2.15) определяют скоростную девиацию курсового гироскопа. Вследствие скоростной девиации ось курсового гироскопа отклоняется от горизонтального положения с угловой скоростью р и изменяет свое направление относительно меридиана с угловой скоростью Девиации, вызванные дебалансом гироскопа. Проекции момента силы тяжести В курсовом гироскопе ось z, направленная по главной оси гироскопа, располагается приблизительно горизонтально. Поэтому в данном случае проекция ускорения Положение осей x и у в плоскости, перпендикулярной главной оси гироскопа, может быть произвольным. Направим одну из осей, например ось у, вертикально вверх. Будем иметь Чтобы определить девиацию курсового гироскопа, вызванную его дебалансом, подставим значения
Знак угловой скорости На рис. 2.14 показано направление Is
Рис. 2.14. Прецессия курсового гироскопа, вызванная дебалансом
На девиацию курсового гироскопа также влияет трение в опорах подвеса гироскопа. Характер девиации курсового гироскопа, вызванной трением, аналогичен характеру девиации гировертикали. СВОБОДНЫ ГИРОСКОП С КОРРЕКЦИЕЙ 3.1. Назначение и принцип работы системы коррекции гироскопа При использовании свободного гироскопа в целях ориентировки на Земле главная ось гироскопа должна устанавливаться в определенное положение относительно Земли. Ручная коррекция положения гироскопа неудобна, а на беспилотных ЛА вообще невозможна. Принцип автоматической коррекции состоит в том, что при отклонении оси гироскопа от требуемого положения создается корректирующий момент, воздействующий на гироскоп и возвращающий его ось в требуемое положение. Устройства, воспринимающие отклонение оси гироскопа от требуемого положения, называют датчиками сигнала коррекции. Устройства, создающие корректирующие моменты, называют моторами коррекции.
Рис. 3.1. Схема автоматической коррекции гироскопа
В гироскопе, подвешенном в кардановом подвесе, датчики сигнала коррекции часто связывают с осями подвеса гироскопа, относительно этих же осей с помощью моторов коррекции создаются корректирующие моменты. На рис. 3.1 показана принципиальная схема системы автоматической коррекции гироскопа, подвешенного в кардановом подвесе. В требуемое положение ось гироскопа устанавливается соответствующим поворотом рам подвеса. Датчик сигнала коррекции
Рис. 3.1 Схема автоматической коррекции гироскопа
Аналогично с помощью датчика сигнала коррекции В курсовых системах в качестве чувствительного элемента используется магнитная стрелка, которая автоматически устанавливается в плоскости магнитного меридиана Земли. Система коррекции, использующая магнитное поле Земли, называется магнитной коррекцией. Курсовая система с магнитной системой коррекции называется гиромагнитным компасом.
|


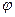 , а главная ось гироскопа в начальный момент расположена горизонтально и образует с касательной С-Ю к линии меридиана угол
, а главная ось гироскопа в начальный момент расположена горизонтально и образует с касательной С-Ю к линии меридиана угол  .
.
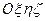 . Ось
. Ось 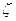 этой системы совместим с начальным направлением оси гироскопа. Ось
этой системы совместим с начальным направлением оси гироскопа. Ось  направим вертикально вверх, а ось
направим вертикально вверх, а ось 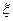 - горизонтально, так чтобы образовалась правая система отсчета.
- горизонтально, так чтобы образовалась правая система отсчета. , равной угловой скорости Земли. Как видно из рис. 2.11, проекциями вектора угловой скорости
, равной угловой скорости Земли. Как видно из рис. 2.11, проекциями вектора угловой скорости  ,
,  .
. . Учитывая это, найдем
. Учитывая это, найдем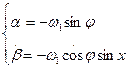 (2.12)
(2.12)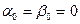 получим
получим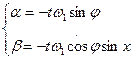 (2.13)
(2.13)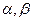 . Угол
. Угол  и его производная
и его производная 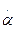 характеризуют девиацию курсового гироскопа в горизонтальной плоскости
характеризуют девиацию курсового гироскопа в горизонтальной плоскости  и его производная
и его производная 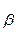 определяют отклонение главной оси гироскопа от плоскости горизонта.
определяют отклонение главной оси гироскопа от плоскости горизонта. , и девиация гироскопа в горизонтальной плоскости будет происходить по ходу часовой стрелки в направлении, противоположном показанному на рис. 2.12. При этом на полюсе, где девиация будет наиболее интенсивной, угловая скорость
, и девиация гироскопа в горизонтальной плоскости будет происходить по ходу часовой стрелки в направлении, противоположном показанному на рис. 2.12. При этом на полюсе, где девиация будет наиболее интенсивной, угловая скорость  , т.е. равна по модулю угловой скорости вращения Земли (15’/ мин). На экваторе
, т.е. равна по модулю угловой скорости вращения Земли (15’/ мин). На экваторе 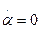 . При переходе в южное полушарие видимое направление девиации в горизонтальной плоскости изменяется на противоположное.
. При переходе в южное полушарие видимое направление девиации в горизонтальной плоскости изменяется на противоположное. (рис. 2.13) составляющие
(рис. 2.13) составляющие 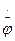 и
и  угловой скорости [см. формулы (2.4) -(2.5)] вращения трехгранника
угловой скорости [см. формулы (2.4) -(2.5)] вращения трехгранника  (2.14)
(2.14) в уравнения (1.15). При
в уравнения (1.15). При 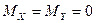 найдем
найдем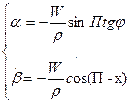 (2.15)
(2.15)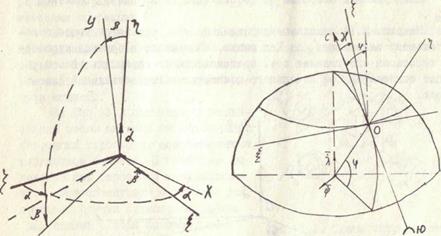
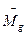 на оси х и у определяются равенствами (2.9).
на оси х и у определяются равенствами (2.9). силы тяжести на ось z близка нулю:
силы тяжести на ось z близка нулю: 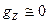 .
. ,
,  . Следовательно,
. Следовательно,  ,
,  .
. ,
, 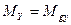 в уравнения (1.15), положив в них
в уравнения (1.15), положив в них 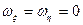 . Получим
. Получим
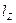 .
.
 связан с осью внешней рамки подвеса гироскопа и управляет мотором коррекции
связан с осью внешней рамки подвеса гироскопа и управляет мотором коррекции 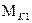 , создающим момент относительно оси внутренней рамки подвеса гироскопа. При отклонении внешней рамки подвеса от требуемого положения создается корректирующий момент относительно оси внутренней рамки. Под действием этого момента гироскоп начинает прецессировать. При этом в соответствии с правилом прецессии главная ось гироскопа будет вращаться вокруг оси внешней рамки, увлекая за собой эту рамку. Прецессия прекратится, когда внешняя рамка возвратится в требуемое положение.
, создающим момент относительно оси внутренней рамки подвеса гироскопа. При отклонении внешней рамки подвеса от требуемого положения создается корректирующий момент относительно оси внутренней рамки. Под действием этого момента гироскоп начинает прецессировать. При этом в соответствии с правилом прецессии главная ось гироскопа будет вращаться вокруг оси внешней рамки, увлекая за собой эту рамку. Прецессия прекратится, когда внешняя рамка возвратится в требуемое положение.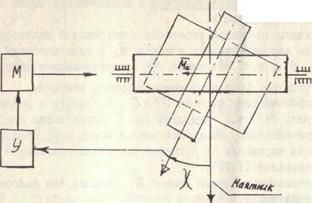
 и мотора коррекции
и мотора коррекции 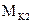 корректируется положение главной оси гироскопа относительно оси внутренней рамки подвеса (рис. 3.1).
корректируется положение главной оси гироскопа относительно оси внутренней рамки подвеса (рис. 3.1).


