Применение свободного гироскопа в качестве гироскопической вертикали
Гироскопическая вертикаль (гирогоризонт) представляет собой свободный гироскоп с вертикально расположенной главной осью и используется как начало отсчета для измерения углов, отсчитываемых от вертикали или горизонта. В идеальном случае главная ось гировертикали должна занимать строго вертикальное положение, но вследствие вращения Земли и некоторых других причин она постоянно отклоняется от этого положения. Это явление называют девиацией гировертикали.
Рис. 2.3. Суточная прецессия гировертикали Ддя исследования девиации гировертикали со свободным гироскопом воспользуемся системой координат Оси Девиация, вызванная вращением Земли. Положение точки 0 относительно Земли остается неизменным. При этом система координат Обозначим угловую скорость Земли
Подставим значения
Проинтегрируем уравнения (2.2) по времени при начальных условиях
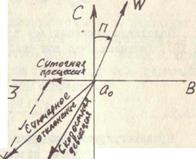
Системы уравнений (2.1) и (2.3) определяют девиацию гировертикали вследствие вращения Земли. Из уравнений (2.3) и рис. 2.4 видно, что вследствие вращения Земли верхний конец главной оси, т.е. вершина гировертикали, отклоняется от плоскости меридиана к западу, а нижний конец оси -к востоку. Скорость отклонения зависит от
Рис. 2.4. Отклонение вершины гировертикали вследствие суточной прецессии Скоростная девиация. Девиация гироскопа, вызванная движением точки опоры 0 относительно Земли, называется скоростной девиацией, ибо зависит от величины и направления скорости точки 0. Если гироскоп установлен на ЛА, то точка опоры гироскопа_ (точка 0) будет перемещаться относительно Земли со скоростью Вектор
Составляющая
где
Рис. 2.5. Составляющие путевой скорости При движении точки О по параллели будет изменяться долгота точки 0. Система отсчета
Таким образом, при движении точки опоры гироскопа 0 относительно Земли, система отсчета Направления векторов
Подставим значения
Проинтегрируем уравнения (2.7) по времени, считая W и П постоянными. При нулевых начальных условиях, т.е. при
Системы уравнений (2.7) и (2.8) определяют скоростную девиацию гировертикали со свободным гироскопом. Скоростная девиация гировертикали показана на рис. 2.6. Как следует из уравнений (2.8), Поэтому результирующее отклонение вершины гироскопа, равное На рис. 2.7 показано суммарное отклонение вершины гироскопа, вызванное вращением Земли и движением ЛА (точки опоры гироскопа 0) относительно Земли. Возникновение скоростной девиации гировертикали со свободным гироскопом можно объяснить следующим образом. При движении точки опоры гироскопа относительно Земли направление местной вертикали, проходящей через эту точку, в инерциальном пространстве постоянно меняется, а положение гировертикали в инерциальном пространстве остается неизменным. Поэтому при движении точки опоры гироскопа относительно Земли гировертикаль будет "отставать" от местной вертикали.
Рис. 2.6. Отклонение вершины гировертикали вследствие скоростной девиации
Рис. 2.7. Суммарное отклонение вершины гировертикали
Девиация, вызванная дебалансом гироскопа. Создать абсолютно уравновешенный гироскоп практически невозможно, ибо вследствие погрешности статической балансировки гироскопа всегда имеет место смещение центра массы гироскопа относительно точки опоры, или, как говорят, имеет место дебаланс гироскопа. Пусть центр массы гироскопа 0 смещен относительно его точки опоры 0 на величину
Рис. 2.8. Момент силы тяжести
Проекции момента силы тяжести на оси ху
Составляющая Поскольку ось z направлена по главной оси, то приближенно можно считать, что Подставив значения Как видим, в данном случае существенное значение имеет смещение центра массы гироскопа в плоскости Оху, перпендикулярной главной оси гироскопа. Смещение центра массы гироскопа в направлении главной оси имеет меньшее значение и в первом приближении его можно не учитывать. Чтобы определить девиацию гировертикали, вызванную дебалансом, достаточно подставить значения
После интегрирования уравнений (2.10) полагая
Уравнения (2.10) и (2.II) определяют девиацию гировертикали, вызванную ее дебалансом. Влияние трения в подвесе на девиацию. На рис. 2.9 показаны векторы угловой скорости основания
Рис. 2.9. Прецессия гироскопа, вызванная трением в опорах
При вращении основания вокруг оси внутренней рамки подвеса гироскоп будет прецессировать вокруг оси внешней рамки. Характер девиации гироскопа, вызванной моментом трения в опорах подвеса, зависит от режима полета ЛА, на котором установлен гироскоп. При режиме, близком к установившемуся, вращение основания относительно оси гироскопа определяется колебаниями ЛА вокруг центра массы. Поэтому вектор момента трения будет совпадать по направлению с вектором угловой скорости вращения ЛА при его колебаниях относительно центра массы. Но при колебаниях направление вращения постоянно меняется, поэтому постоянно будет изменяться и направление момента трения: момент трения будет знакопеременным. Знакопеременный момент трения вызывает колебания главной оси гироскопа. Но так как момент трения невелик, а направление его меняется с достаточно высокой частотой, то при малой скорости прецессии гироскопа амплитуда колебаний гироскопа, вызванных моментом трения, будет мала. Отсюда, однако, не следует, что трение в опорах подвеса гироскопа не имеет существенного значения. Трение в опорах подвеса определяет точность статической балансировки гироскопа. Поэтому для повышения качества статической балансировки необходимо по возможности уменьшать трение в опорах подвеса гироскопа.
|


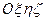 (рис. 2.3), начало которой поместим в закрепленной точке гироскопа. Ось
(рис. 2.3), начало которой поместим в закрепленной точке гироскопа. Ось 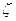 в данном случае направим вертикально вверх. Используем при анализе системы уравнений (I.I4) и (I.I5), справедливые только для малых углов
в данном случае направим вертикально вверх. Используем при анализе системы уравнений (I.I4) и (I.I5), справедливые только для малых углов  .
. горизонтальны. Для простоты одну из осей, например ось
горизонтальны. Для простоты одну из осей, например ось 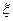 , целесообразно направить по касательной к меридиану с юга на север. Ось
, целесообразно направить по касательной к меридиану с юга на север. Ось  окажется направленной по касательной к параллели с востока на запад.
окажется направленной по касательной к параллели с востока на запад. и спроектируем вектор
и спроектируем вектор  на оси
на оси 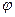 - широта места точки 0. Тогда
- широта места точки 0. Тогда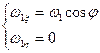 (2.1)
(2.1)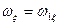 и
и 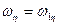 уравнения (1.15). Учитывая, что для свободного гироскопа
уравнения (1.15). Учитывая, что для свободного гироскопа 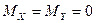 noлучим
noлучим (2.2)
(2.2)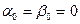 . Получим
. Получим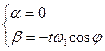 (2.3)
(2.3)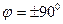 вращение Земли на приводит к девиации гировертикали.
вращение Земли на приводит к девиации гировертикали.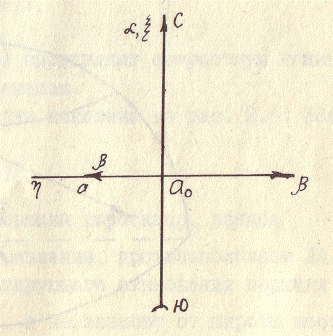 J
J 
 , равной путевой скорости ЛА. Для исследования скоростной девиации достаточно рассмотреть только горизонтальное движение точки 0, т.е. считать вектор
, равной путевой скорости ЛА. Для исследования скоростной девиации достаточно рассмотреть только горизонтальное движение точки 0, т.е. считать вектор 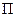 (рис. 2.5). Разложим вектор
(рис. 2.5). Разложим вектор  и восточную"
и восточную"  составляющие:
составляющие: ,
,  .
.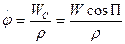
 - расстояние от точки О до центра Земли.
- расстояние от точки О до центра Земли.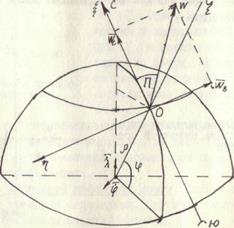
 (2.5)
(2.5) получает дополнительное вращение с угловой скоростью
получает дополнительное вращение с угловой скоростью  .
. показаны на рис. 2.5. Найдем
показаны на рис. 2.5. Найдем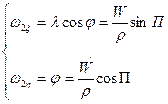 (2.6)
(2.6) и
и  в уравнения (1.15). Учитывая, что для свободного гироскопа
в уравнения (1.15). Учитывая, что для свободного гироскопа 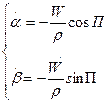 (2.7)
(2.7)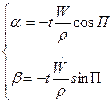 (2.8)
(2.8) .
. , будет происходить в направлении, противоположном ЛА, т.е. вектору
, будет происходить в направлении, противоположном ЛА, т.е. вектору 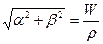 и не зависит от широты места и направления движения ЛА.
и не зависит от широты места и направления движения ЛА.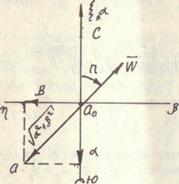
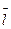 (рис. 2.8). Б таком случае относительно точки опоры 0 появится момент силы тяжести
(рис. 2.8). Б таком случае относительно точки опоры 0 появится момент силы тяжести

 (2.9)
(2.9)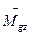 момента силы тяжести значения не имеет, так как направлена по главной оси гироскопа и прецессии гироскопа не вызывает.
момента силы тяжести значения не имеет, так как направлена по главной оси гироскопа и прецессии гироскопа не вызывает. ,
, 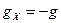 .
.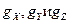 в систему уравнений (2.9),
в систему уравнений (2.9), и
и 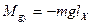
 ,
, 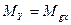 в уравнения (1.15), положив в них
в уравнения (1.15), положив в них 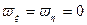 . Выполнив эту подстановку, найдем
. Выполнив эту подстановку, найдем
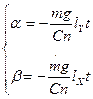 (2.11)
(2.11) относительно главной оси гироскопа и момента трения
относительно главной оси гироскопа и момента трения 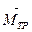 в предположении, что основание гироскопа вращается вокруг оси внешней рамки подвеса гироскопа. Момент трения вызывает прецессию гироскопа вокруг оси внутренней рамки подвеса. Направление прецессии гироскопа для данного случая показано на рис. 2.9 стрелкой.
в предположении, что основание гироскопа вращается вокруг оси внешней рамки подвеса гироскопа. Момент трения вызывает прецессию гироскопа вокруг оси внутренней рамки подвеса. Направление прецессии гироскопа для данного случая показано на рис. 2.9 стрелкой.



