Модели оценки эффективности отдельных инструментов фондового рынка
Эффективность любых инвестиций определяется на основе сопоставления эффекта (дохода) и затрат. В качестве затрат при определении эффективности финансовых вложений выступают средства, инвестированные в различные фондовые инструменты. В качестве эффекта или дохода выступает разница между реальной стоимостью отдельных фондовых инструментов и суммой средств, инвестированных на их приобретение. Так как эффект или доход от этих инвестиций может быть получен лишь в будущем периоде, он должен быть оценен при сравнении в настоящей стоимости. Таким образом, принципиальная формула для расчета финансовых инвестиций будет иметь вид Эф=
где Эф - эффективность инвестирования в инструменты фондового рынка, %; РСф - реальная стоимость отдельных фондовых инструментов (приведенная к настоящей стоимости); Иф - сумма средств, инвестированных в отдельные фондовые инструменты (или намечаемых к инвестированию). Разность (РСф-Иф) представляет собой при этом сумму ожидаемого дохода от инвестиций (Дф). Поэтому формулу можно переписать так Эф = (6.12)
Реальную настоящую стоимость фондовых инструментов определяют следующие показатели: 1. Сумма будущего денежного потока от конкретного вида фондового инструмента; 2. Размер дисконтной ставки, используемой при оценке настоящей стоимости будущего денежного потока. I Сумма будущего денежного потока по финансовым инвестициям формируется по иным принципам, чем по реальным инвестициям. В связи с отсутствием основных фондов в составе будущего денежного потока по финансовым инвестициям нет амортизационных отчислений. В качестве же чистой прибыли по финансовым инвестициям выступает чистый доход. Формирование будущего денежного потока по отдельным видам фондовых инструментов имеет существенные отличительные особенности. По облигациям, сберегательным сертификатам и другим аналогичным кредитным инструментам сумма будущего денежного потока складывается из суммы поступления процентов по этим активам и стоимости самого актива на момент его погашения. При этом возможны три принципиальных варианта формирования будущего денежного потока по этим видам фондовых инструментов: 1. Без выплаты процентов по фондовому инструменту. Данный вид кредитного фондового инструмента обеспечивает инвестору лишь один вид дохода – разность между объявленной выкупной ценой по нему и ценой приобретения; 2. С периодической выплатой процентов и погашения в конце предусмотренного срока. Это наиболее распространенный в настоящее время вариант эмитирования этих фондовых инструментов; 3. С выплатой всей суммы процентов при погашении в конце предусмотренного срока. По акциям и инвестиционным сертификатам сумма будущего денежного потока формируется в зависимости от двух условий: 1) При использовании фондового инструмента в течение неопределенного продолжительного периода времени (в виде долгосрочного финансового актива). В этом случае денежный поток будущего периода формируется исключительно за счет сумм начисляемых дивидендов; 2) При использовании фондового инструмента в течение заранее предусмотренного срока (например, по инвестиционным сертификатам закрытых инвестиционных фондов). В этом случае будущий денежный поток складывается из сумм поступлений дивидендов. Как в первом, так и во втором вариант формирования денежного потока по акциям и инвестиционным сертификатам наиболее постоянным его источником выступают выплачиваемые дивиденды. В зависимости от условий обращения фондовых инструментов данного вида, стадии развития компании - эмитента, разработанной дивидендной политики и других факторов возможна различная динамика уровня выплачиваемых дивидендов в предстоящем периоде. В этой связи акции и инвестиционные сертификаты делятся на группы: а) Со стабильным уровнем дивидендов. Наиболее типичным примером таких финансовых инструментов являются привилегированные акции. Однако такими могут быть и простые акции и инвестиционные сертификаты. б) С постоянно возрастающим уровнем дивидендов. Дивидендная политика многих эмитентов предусматривает ежегодный прирост суммы или процента выплачиваемых дивидендов на определенную постоянную величину. в) С непостоянным уровнем дивидендов. Такая дивидендная политика наиболее часто предусматривается компанией-эмитентом при смене стадий ее жизненного цикла. Так, при переходе из стадии "детства" в стадию "юность" динамика уровня дивидендов может носить прогрессирующий характер; при переходе из стадии "юность" в стадию "ранняя зрелость" она, наоборот, будет носить регрессирующий характер. II. Размер дискетной ставки, используемой при оценке настоящей стоимости суммы будущего денежного потока, также играет важную роль при оценке эффективности финансовых инвестиций. Использовать единую, "усредненную" ставку процента в этих целях нельзя, так как при оценке инвестиционных качеств отдельных фондовых инструментов было показано, что уровень риска по ним существенно колеблется. Следовательно, с учетом премии за риск ставка процента, используемая при дисконтировании денежного потока, также должна быть дифференцирована. Часто эту ставку процента называют норма «текущей доходности». Дифференциация нормы текущей доходности при определении настоящей стоимости денежного потока по отдельным фондовым инструментам осуществляется с учетом следующих показателей: а)ставки ссудного (кредитного) процента на региональном денежном рынке; б)предполагаемого темпа инфляции в предстоящем периоде; в)премии за инвестиционный риск по конкретным фондовым инструментам. Первые два показателя формируют норму текущей доходности по так называемым «безрисковым финансовым инвестициям», в частности, по облигациям внутреннего государственного займа. Норма текущей доходности по безрисковым финансовым инвестициям может рассматриваться как единый базис для последующей дифференциации дисконтной ставки по конкретным фондовым инструментам. В соответствии с принципом "Ценовой модели капитальных активов" (раздел 2.3), норма текущей доходности по конкретному фондовому инструменту определяется как сумма нормы текущей доходности по безрисковым инвестициям и нормы премии за риск (риск повышения ставки ссудного процента; риск повышения предполагаемого темпа инфляции; риск неплатежа и т.п.). Уровень этих рисков определяет в конечном итоге степень дифференциации нормы текущей доходности по отдельным фондовым инструментам. Рассмотрим подробно модели оценки реальной стоимости отдельных фондовых инструментов. Оценка облигаций (сберегательных сертификатов и других аналогичных ценных бумаг) предусматривает решение ряда задач, среди которых важнейшей является определение ее текущей рыночной стоимости. Формула, по которой рассчитывается этот показатель, называется основной моделью оценки облигации" (Ваsiс Воnd. Valuation Model). Она имеет вид: Сот = где Сот - текущая рыночная стоимость облигации; По - ежегодная сумма процента по облигациям, представляющая собой произведение ее номинала на объявленную ставку процента. Если сумма процента выплачивается с иной периодичностью, то расчет по формуле производится с предусматриваемыми периодами выплаты процента; Но - номинал облигации, подлежащей погашению в конце периода ее обращения; НД - норма текущей доходности, используемая как дисконтная ставка в расчетах настоящей стоимости в десятичной дроби; n - число лет (или иных периодов), оставшихся до погашения облигации. Экономическое содержание основной модели оценки облигаций заключается в том, что ее текущая рыночная стоимость равна сумме всех процентных поступлений за оставшийся период ее обращения и номинала, дисконтированных по норме текущей доходности для данного вида облигаций. Пример: На фондовом рынке предлагается к продаже облигация одной из компаний по цене 90 тыс. руб. за единицу. Она была выпущена сроком на 3 года, до погашения осталось 2 года. Ее номинал при выпуске определен в 100 тыс. руб. Процентные выплаты по облигации осуществляются один раз в год по ставке 30% к номиналу. С учетом уровня риска данного типа облигации норма ее текущей доходности принимается в размере 35% в год. Необходимо определить текущую рыночную стоимость облигации и ее соответствие цене продажи. Подставив в формуле эти данные, получим:
Сопоставив эту величину с ценой продажи 90 тыс. руб., мы видим, что кроме текущей рыночной стоимости по ней можно получить дополнительно 3,6 тыс.руб. Наряду с оценкой текущей рыночной стоимости облигации перед инвестором возникают задачи определения их ожидаемой доходности. Как уже отмечали, существуют три принципиальных варианта, для которых существуют соответствующие модели расчета ожидаемой доходности облигаций. Модель расчета ожидаемой доходности по облигациям без выплаты процентов имеет следующий вид: ДОбп где ДОбп - ожидаемая доходность по облигациям без выплаты процентов, в десятичной дроби; Но - номинал облигации, подлежащей погашению в конце периода ее обращения; ЦПо - цена, по которой облигация реализуется на рынке: n - число лет, остающихся до погашения облигации. Экономическое содержание данной модели состоит в том, что уровень ожидаемой доходности по облигациям без выплаты процентов представляет собой дисконтную ставку, по которой номинал облигации приводится к настоящей стоимости, приравненной к цене ее реализации. Пример: Облигация внутреннего местного займа номиналом в 100 тыс. руб. реализуется по цене 67,5 тыс. руб. Погашение облигации предусмотрено через 3 года. Норма текущей доходности по облигациям такого типа составляет 16%. Необходимо определить ожидаемую доходность по облигации и ее соответствие текущей норме доходности облигации такого типа. Подставив данные в формулу, имеем
ДОбп
Сопоставив полученную ожидаемую доходность, 14%, с текущей нормой доходности по облигациям такого типа, 16%, видно, что уровень доходности по предлагаемой облигации ниже среднерыночной. Соответственно, модель расчета текущей рыночной стоимости облигации без выплаты процентов имеет вид: СОбп = где СОбп - текущая рыночная стоимость облигации без выплаты процентов; Но - номинал облигации, подлежащей погашению в конце периода ее обращения; НД - норма текущей доходности по конкретному виду облигаций (в десятичной дроби); n - число лет. остающихся до погашения облигации. Экономическое содержание данной модели состоит и том, что текущая рыночная стоимость облигации без выплаты процентов представляет собой ее номинал, приведенный к настоящей стоимости по дисконтной ставке, равной норме текущей доходности по ней. Эта модель представляет собой упрощенный вариант основной модели оценки облигации (ее вторая часть). Пример: Необходимо определить текущую рыночную стоимость облигации внутреннего местного займа и сопоставить ее с ценой продажи„используя исходные данные предыдущего примера.. Подставляя эти данные в формулу (6.15) получим: СОбп Сопоставляя эту величину с ценой продажи облигации (67,5-63,9=3,6), видим, что она завышена на 3,6 тыс. руб. Модель расчета ожидаемой текущей доходности по облигациям с периодической выплатой процентов имеет следующий вид: ДОпп где ДОпп - ожидаемая текущая доходность по облигации с периодической выплатой процентов в десятичной дроби. Но - номинал облигации, к которому начисляется сумма процента; ПС — ставка, по которой начисляется сумма процента по облигации в десятичной дроби; ЦПo - цена, по которой облигация реализуется на рынке. Экономическое содержание данной модели состоит в том, что уровень ожидаемой текущей доходности по облигации с периодической выплатой процентов представляет собой частное от деления ежегодной суммы процента на ее рыночную цену. Необходимость дисконтирования в этом случае отпадает, так как оба указанных показателя должны приводится к настоящей стоимости по единой ставке дисконта, в результате чего их соотношения не изменится. Что касается расчета текущей рыночной стоимости таких облигаций, то в этих целях используется Основная модель оценки облигации. Пример: Облигация компании номиналом 2ОО тыс. руб. реализуется на рынке по цене 225 тыс. py6. Ставка ежегодного начисления процентов по ней составляет 40%. Норма текущей доходности по облигациям такого типа составляет 35%. Необходимо определить ожидаемую текущую доходность по облигации, сопоставив ее с нормой текущей доходности. Подставив в формулу данные величины, получим ожидаемую текущую доходность по облигации: ДОпп Сопоставляя ожидаемую и нормативную текущую доходность по облигации, мы видим, что они примерно одинаковы (35,6% и 35%). Модель расчета ожидаемой текущей доходности по облигациям с выплатой всей суммы процентов при погашении имеет следующий вид: ДОпк =
где ДОпк - ожидаемая текущая доходность по облигации с выплатой всей суммы процентов при погашении в десятичной дроби: ЦПо — цена, по которой облигации реализуются на рынке; Но - номинал облигации, к которому при погашении будет начислена сумма процента; ПСк - ставка. по которой будет начислена сумма процента по облигации при ее погашении, в десятичной дроби. Экономическое содержание данной модели состоит в том, что уровень ожидаемой текущей доходности по облигации с выплатой всей суммы процентов при ее погашении представляет собой частное от деления общего коэффициента выплат при погашении по отношению к номиналу на номинал облигации, приведенный к настоящей стоимости, равной цене ее реализации. Модель расчета текущей рыночной стоимости облигаций с выплатой всей суммы процентов при погашении имеет следующий вид: СОпк= где СОпк - текущая рыночная стоимость облигации с выплатой всей суммы процентов при погашении; Hо - номинал облигации, подлежащей погашению в конце периода ее обращения; Пк - сумма процента по облигации, которая будет начислена при ее погашении по соответствующей ставке; НD - норма текущей доходности, используемая как дисконтная ставка в расчетах настоящей стоимости, в десятичной дроби; n - число лет, остающихся до погашения облигации. Экономическое содержание данной модели состоит в том, что текущая рыночная стоимость облигации равна совокупным выплатам номинала и суммы процента при погашении, дисконтированным по норме текущей доходности для данного вида облигаций. Она также представляет собой упрощенный вариант основной модели оценки облигаций (где ее первая часть представляет собой разовый платеж). Пример: Облигация компании номиналом в 100 тыс. руб. реализуется на рынке по цене 67,5 тыс. руб. Погашение облигации и разовая выплата суммы процента по ней по ставке 20% предусмотрены через 3 года. Норма текущей доходности по облигациям такого типа составляет 35%. Необходимо определить ожидаемую текущую доходность и текущую рыночную стоимость данной облигации. Подставив в формулу модели ожидаемой текущей доходности данного типа облигаций соответствующие значения показателей, получим: ДОпк Соответственно, подставив необходимые показатели в формулу модели текущей рыночной стоимости, получим: COпк =
В зарубежной практике для быстрой ориентации инвесторов в определении текущей доходности и текущей рыночной стоимости облигаций с различными ценами реализации и ставками процентных платежей используются специальные таблицы, называемые 'книги доходности облигаций" («Yield Books»). Вышеперечисленные методы оценки облигаций полностью применимы к расчету аналогичных показателей по сберегательным сертификатам и другим кредитным ценным бумагам. Оценка акций (и инвестиционных сертификатов) направлена прежде всего на определение их текущей рыночной стоимости. Особенно актуальна эта задача для условий нашего фондового рынка, где рыночная цена продажи акций многих компаний и банков значительно превышает их реальную текущую рыночную стоимость. Рассмотрим основные модели, используемые при определении текущей рыночной стоимости акций (а также инвестиционных сертификатов). Модели оценки текущей рыночной стоимости акции при ее использовании в течение неопределенного продолжительного периода времени имеет вид:
САтн =
где САтп - текущая рыночная стоимость акции, используемой неопределенное число лет; Dn - сумма дивидендов, которую инвестор ожидает получить в n-ом году; HD - норма текущей доходности акций данного типа, используемая как дисконтная ставка в расчетах настоящей стоимости, в десятичной дроби; n - число лет, включенных в расчет. Экономическое содержание данной модели состоит в том, что текущая рыночная стоимость акции, используемой неопределенное число лет, представляет собой сумму дивидендов по отдельным периодам, приведенную к настоящей стоимости по дисконтной ставке, равной норме текущей доходности по ней. Пример: Приобретенная инвестором акция представляется инвестору перспективной и намечена им к использованию в течение продолжительного периода. На ближайшие пять лет им составлен прогноз дивидендов, в соответствии с которым в первый год сумма дивидендов составит 100 тыс. руб., а в последующие годы будет ежегодно возрастать на 20 тыс. руб. Норма текущей доходности акций данного типа составляет 15% в год. Необходимо определить текущую рыночную стоимость акции. Подставив данные в формулу, получим: CАт Применительно к нашим условиям рассмотренный вариант представляет собой лишь гипотетический случай, так как ни один инвестор не планирует держать свои финансовые активы столь продолжительное время и уж тем более не сможет составить столь длительный прогноз получения дивидендов в условиях нашей экономики. Более типичная ситуация, когда. денежный поток будет состоять не только из дивидендов, но и возрастающей стоимости акции при ее реализации. Модель опенки текущей рыночной стоимости акций при их использовании в течение заранее предусмотренного срока имеет вид: САто= где CAтo - текущая рыночная стоимость акции, используемой заранее предусмотренный период; Dn - сумма дивидендов, которую инвестор ожидает получить в n-ом году; ЦРа - прогнозируемая рыночная цена реализации акции в конце периода ее использования; НD - норма текущей доходности акций данного типа, используемая как дисконтная ставка в расчетах настоящей стоимости, в десятичной дроби; n - число лет использования акции. Экономическое содержание данной модели аналогично основной модели оценки облигаций. Отличия состоят лишь в том, что вместо суммы процентов используются показатели дифференцированной по годам суммы дивидендов, а вместо номинала облигации - прогнозируемая рыночная цена акции в момент ее реализации. Сам же механизм расчета текущей рыночной стоимости при этом не меняется. Основу как первой, так и второй модели оценки текущей рыночной стоимости акций составляет дисконтированная сумма дивидендов, ожидаемая к получению в предстоящем периоде. При этом сумма ежегодных дивидендов может оставаться неизменной. равномерно возрастать или меняться по отдельным периодам. Оценка акций в этом случае носит дифференцированный характер. Модель оценки текущей рыночной стоимости акций с постоянными дивидендами имеет вид: САn =
Где САn – текущая рыночная стоимость акции с постоянными дивидендами; D- годовая сумма постоянного дивиденда; HD – норма текущей доходности акций данного типа, в десятичной дроби. Пример:По акции выплачивается ежегодный постоянный дивиденд в сумме 200 тыс. руб. Норма текущей доходности акций данного типа составляет 25 % в год. Текущая рыночная стоимость акции равна
САп = Модель оценки текущей рыночной стоимости акций с постоянно возрастающими дивидендами («Модель Гордона») имеет вид:
САпв = Где САпв – текущая рыночная стоимость акции с постоянно возрастающими дивидендами; Do – сумма последнего уплаченного дивиденда; HD – норма текущей доходности акций данного типа, в десятичной дроби; Пd – темп роста дивидендов, в десятичной дроби. Пример: Последний дивиденд, выплаченный по акции, составляет 150 тыс.руб. Компания постоянно увеличивает сумму ежегодно выплачиваемых дивидендов на 10 %. Норма текущей доходности акций данного типа составляет 20 % в год. Текущая рыночная стоимость будет составлять: САпв =
Модель оценки текущей рыночной стоимости акций с изменяемой суммой дивидендов по периодам имеет вид:
САпв =
где CAпв - текущая рыночная стоимость акции с изменяемой суммой дивидендов; Dn — сумма дивидендов, прогнозируемая в n-ом периоде; HD - норма текущей доходности акций данного типа, в десятичной дроби; n - число прогнозируемых лет. Пример: В соответствии с принятой дивидендной политикой компания ограничила выплату дивидендов в предстоящие три года суммой 30 тыс. руб. в год. В последующие пять лет она обязалась выплачивать постоянные дивиденды в размере 100 тыс. руб в год. Норма текущей доходности акций данного типа составляет 25% в год. Текущая рыночная стоимость акции будет CAпв Модели оценки реальной рыночной стоимости и текущей доходности отдельных фондовых инструментов используются при их выборе и включении в формируемый инвестиционный портфель. ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ ПО ТЕМЕ Какие фондовые инструменты пользуются наибольшим интересом инвесторов сегодня? По каким признакам классифицируются акции? Какие параметры исследуются при оценке инвестиционных качеств конкретных акций? Какие виды облигаций существуют? По каким признакам отличаются сберегательные сертификаты? Какое экономическое содержание инвестиционных сертификатов? Какие принципиальные варианты существуют при оценке рыночной стоимости и ожидаемой доходности облигаций? Какие возможные варианты возникают при оценке текущей рыночной стоимости акций?
|

 (6.11)
(6.11)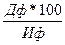 . (6.12)
. (6.12) (6.13)
(6.13)
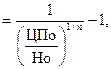 (6.14)
(6.14)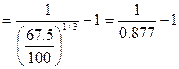 = О,14 (или 14%).
= О,14 (или 14%). , (6.15)
, (6.15)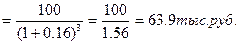
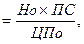 (6.16)
(6.16)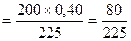 = 0,35б (или 35,6%)
= 0,35б (или 35,6%)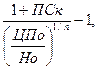 (6.17)
(6.17)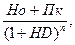 (6.18)
(6.18)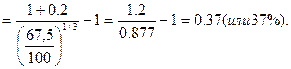
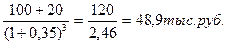
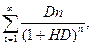 (6.19)
(6.19) 87,0+90,9+92,1+91,4+89,6=451,0
87,0+90,9+92,1+91,4+89,6=451,0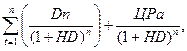 (6.20)
(6.20)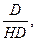 (6.21)
(6.21)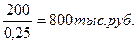
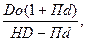 (6.22)
(6.22)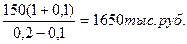
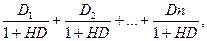 (6.23)
(6.23)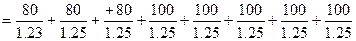 = 592 тыс.руб
= 592 тыс.руб


