Коінтеграція
Коінтеграціоний аналіз тимчасових рядів з'явився в економетрії в середині 1980 років і був сприйнятий багатьма економетристами як найбільш важливе з останніх розробок в емпіричному моделюванні. Базові ідеї й викладення застосування коінтеграційного аналізу вимагають знання й застосування лише методу найменших квадратів і опираються на поняття стаціонарних і нестаціонарних процесів. Нестаціонарність тимчасового ряду завжди була проблемою в економетричному аналізі. Як було показано в ряді теоретичних робіт (Філіпс, 1986), у загальному випадку, статистичні характеристики регресійного аналізу, використовувані для нестаціонарних тимчасових рядів, сумнівно. Якщо змінні, що включаються в модель у якості регресорів, нестаціонарні, то отримані оцінки будуть дуже поганими. Вони не будуть мати властивість заможності, тобто не будуть сходитися по ймовірності до щирих значень параметрів у міру збільшення вибірки. Такі показники, як коефіцієнт детермінації Проілюструвати цей ефект можна на досить абсурдному прикладі: Нехай
а
Для n=30 результат регресії виглядає так:
у дужках наведені значення статистики Стьюдента, Якщо не брати до уваги статистику DW, рівняння регресії виглядає цілком благополучно, хоча й демонструє зовсім помилкову залежність. Свідченням того, що регресія невірна, є дуже низький рівень DW. Цей екстремальний варіант демонструє небезпека інтерпретації регресії для двох детермінованих трендів. Не краще є справа, коли змінні містять стохастичний тренд. Припустимо, що два змінні:
де Розглянемо два рівняння регресії: (a) Між (b) Провівши досить багато реалізацій, наприклад, 50 000, певного розміру (по 50 спостережень, наприклад, кожна), методом Монте-Карло прийдемо до У випадку (а) емпіричний розподіл t-статистики для У випадку (b) емпіричний розподіл t-статистики для У підсумку, якщо використовувати звичні нам таблиці розподілу Стьюдента для перевірки значимості регресії для рядів зі стохастичними трендами, в 2/3 випадків можна одержати, що регресія буде «гарної» (коефіцієнти значимі). І приблизно в 75% випадків буде відкинута вірна гіпотеза про відсутність зв'язку. Аналогічно з іншими коефіцієнтами. Хоча процеси Вищенаведені два приклади показують, чому економісти не люблять будувати регресію для тимчасових рядів зі стахостичним або детермінованим трендом. Використання методу найменших квадратів для оцінювання параметрів і перевірки гіпотез є ефективним лише тоді, коли ряди (процеси) є стаціонарними. Багато економічні змінні перед використанням у регресійному аналізі, піддаються перетворенням. Найбільш зручним способом звільнення від тренда, з обліком сказаного, є перехід до різниць такого порядку, що забезпечує стаціонарність. Для процесів зі стохастичним трендом типу випадкового блукання стаціонарної буде перша різниця:
Аналогічний висновок можна зробити для процесу випадкового блукання із дрейфом.
Іноді необхідно переходити до різниць більше високого порядку, щоб досягти стаціонарності. Наприклад, якщо
те лише друга різниця цього процесу буде стаціонарною:
З позиції цих результатів, особливу важливість здобувають так звані інтегровані процеси. Це поняття пов'язане з іменами Энгл, Гренджер. Нестаціонарний процес, перші різниці якого стаціонарні, називають інтегрованим першого порядку й позначають I(1). Стаціонарний процес позначають I(0). Якщо k-тие різниці випадкового процесу стаціонарні, то його називають інтегрованим k-того порядку й позначають I(k). Процеси випадкового блукання й випадкового блукання із дрейфом - I(1), Процес (1) - інтегрований другого порядку I(2). З усвідомленням небезпеки застосування методу найменших квадратів до нестаціонарних рядів, з'явилася необхідність у тестах, які дозволили б відрізнити стаціонарний процес від нестаціонарного. Неформальні методи тестування стаціонарності нам уже відомі - візуальний аналіз графіків автокореляційої функції й спектральній щільності. Серед формальних тестів найвідомішим у цей час є тест, розроблений Дикі й Фулером (DF = Dickey-Fuller integration test). Але на початку про те, як співвідносяться стаціонарність і одиничні коріння. Розглянемо AR(1), причому визначимо його так:
де Цей процес стаціонарний, якщо
Якщо
Звідки легко видно, що
І математичне очікування, і дисперсія, і автокореляція не залежать від часу. Тобто AR(1) стаціонарен, якщо Представимо цю умову стаціонарності по-іншому: запишемо рівняння AR(1) через оператор авторегресії
Коренем характеристичного рівняння
· І умова · Якщо · Якщо ж Тестування стаціонарності, таким чином, прямо пов'язане з визначенням одиничних корінь.
|

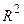 , t-статистики, F-статистики, будуть указувати на наявність зв'язку там, де її насправді немає. Такий ефект називають помилковою регресією.
, t-статистики, F-статистики, будуть указувати на наявність зв'язку там, де її насправді немає. Такий ефект називають помилковою регресією.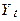 - крапки, що лежать на прямій:
- крапки, що лежать на прямій: 

 на квадратичній лінії:
на квадратичній лінії: 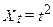
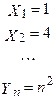

 .
. незалежно сгенеровані процеси випадкового блукання з незалежними нормально розподіленими помилками.
незалежно сгенеровані процеси випадкового блукання з незалежними нормально розподіленими помилками.
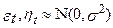 , і
, і 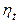 - селестічні числа (стандартні) нормального розподілу.
- селестічні числа (стандартні) нормального розподілу. :
: 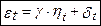
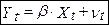
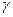 близько до теоретичного розподілу Стьюдента.
близько до теоретичного розподілу Стьюдента.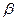 сильно відрізняється від теоретичного розподілу Стьюдента, хоча воно симетрично, стандартне відхилення набагато більше, ніж у розподілу Стьюдента.
сильно відрізняється від теоретичного розподілу Стьюдента, хоча воно симетрично, стандартне відхилення набагато більше, ніж у розподілу Стьюдента.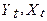 незалежні, регресія (b) з великою ймовірністю дасть високий (через нестаціонарність) коефіцієнт детермінації.
незалежні, регресія (b) з великою ймовірністю дасть високий (через нестаціонарність) коефіцієнт детермінації.
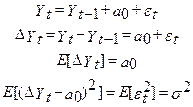
 - процес випадкового блукання
- процес випадкового блукання 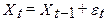 , а
, а  дорівнює:
дорівнює: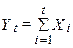 (1)
(1) - нестаціонарна
- нестаціонарна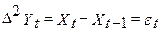 - стаціонарна.
- стаціонарна.
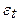 - білий шум.
- білий шум.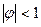 . Це легко доводиться з використанням лагового оператора В.
. Це легко доводиться з використанням лагового оператора В. , тобто нескінченний процес МА.
, тобто нескінченний процес МА.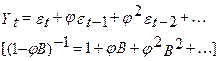
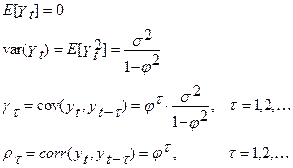
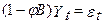
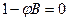 є
є
 ), що говорить про те, що процес стаціонарений;
), що говорить про те, що процес стаціонарений; , або, що то ж саме,
, або, що то ж саме,  , процес вибухової;
, процес вибухової;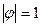 , а це має місце тоді й тільки тоді, коли
, а це має місце тоді й тільки тоді, коли  , умова стаціонарності не виконується. Має місце випадкове блукання, у нестаціонарності якого вже ми переконалися.
, умова стаціонарності не виконується. Має місце випадкове блукання, у нестаціонарності якого вже ми переконалися.


