УСУНЕННЯ ТРЕНДА
Звичайні методу усунення тренда: a) Диференціація (перехід до різниць) b) Детрендизація Детрендизація являє собою побудова регресії по «часі» і одержання залишків. Ми вже випробовували ARIMA(p,d,q), у якій d-танучи різницю рядів стаціонарна. Ціль цього розділу - зрівняти ці два методи виключення тренда. ДИФЕРЕНЦІАЦІЯ (перехід до різниць) Спочатку розглянемо рішення моделі випадкового блукання із дрейфом:
Взявши перші різниці, одержуємо
Цікавий випадок моделі випадкового блукання із шумом. У перших різницях модель може бути записана як
При S=1, коефіцієнт кореляції між
Дослідження виявляє, що Т.к. перші різниці Т.к. додавання константи не впливає на корелограму, те це означає, що модель тренда із шумом також поводиться як ARIMA(0,1,1) процес. Модель локального лінійного тренда поводиться як ARIMA(0,2,2). Взявши перші й другі різниці
так що
Т.к.
Всі інші коваріації дорівнюють нулю. Т.к. локальна лінійна трендова модель поводиться як ARIMA(0,2,2). ДЕТРЕНДИЗАЦІЯ (узяття різниці) Ми показали, як може бути іноді диференціація (перехід до різниці) використана для перетворення нестаціонарної моделі в стаціонарну модель у вигляді ARMA. Це не виходить, що всі нестаціонарні моделі можуть бути перетворені в благополучні ARMA моделі узяттям різниці. Розглянемо, наприклад, модель, що є сумою детермінованого тренда й чистого шуму:
Перша різниця
Тут Замість цього прийнятний шлях для трансформації цієї моделі - оцінити рівняння регресії:
Вирахування оцінних значень У загальному випадку часовий ряд може мати поліноміальний тренд. Процес, отриманий після усунення тренда, може бути піддадуть моделюванню використанням традиційних методів, таких, як ARMA-Оцінювання. Тепер розглянемо загальний клас ARIMA(p,d,q) моделей
де На початку припустимо, що A(L) має єдиний одиничний корінь, а B(L) має всіх корінь поза одиничним колом. Зміст у тім, що перша різниця процесу з одиничним коренем стаціонарна. Якщо A(L) має два одиничних корені, той же самий аргумент може бути використаний, щоб показати, що друга різниця
|


 . Ясно, що послідовність
. Ясно, що послідовність  - рівна константі плюс розподіл білого шуму – стаціонарна. Розглядаючи
- рівна константі плюс розподіл білого шуму – стаціонарна. Розглядаючи 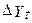 як цікавить змінну, маємо:
як цікавить змінну, маємо: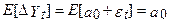
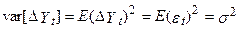

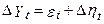 . У такій формі легко показати, що
. У такій формі легко показати, що 
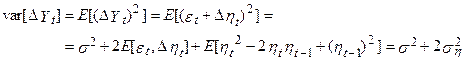


 дорівнює
дорівнює
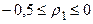 й що всі інші коефіцієнти кореляції дорівнюють нулю.
й що всі інші коефіцієнти кореляції дорівнюють нулю. поводяться точно як MA(1) процес, модель випадкового блукання із шумом – це ARIMA(0,1,1).
поводяться точно як MA(1) процес, модель випадкового блукання із шумом – це ARIMA(0,1,1).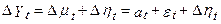

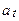 саме по собі нестаціонарно, можна легко показати, що перша різниця
саме по собі нестаціонарно, можна легко показати, що перша різниця  , помітимо:
, помітимо: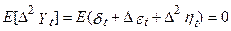
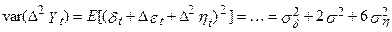

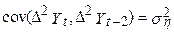

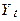 не дуже добре поводиться тому що
не дуже добре поводиться тому що
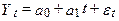
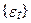 .
.
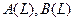 - поліноми лагового оператора L.
- поліноми лагового оператора L.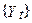 стаціонарна. У загальному випадку d-танучи різницю процесу з d одиничними коріннями стаціонарна. ARIMA(p,d,q) має d одиничних корінь; d-танучи різницю такої моделі - стаціонарний ARMA(p,q) процес. Якщо процес має d одиничних корінь, говорять, що він інтегрований порядку d, або просто I(d).
стаціонарна. У загальному випадку d-танучи різницю процесу з d одиничними коріннями стаціонарна. ARIMA(p,d,q) має d одиничних корінь; d-танучи різницю такої моделі - стаціонарний ARMA(p,q) процес. Якщо процес має d одиничних корінь, говорять, що він інтегрований порядку d, або просто I(d).


