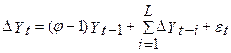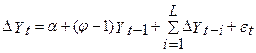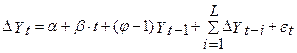Визначення одиничних корінь методом Дикі-Фулера
Дикі й Фулер (1979,1981) розглядають процес AR(1)
Нульова гіпотеза Проти альтернативної Т.е. нульова гіпотеза припускає, що На перший погляд, можна побудувати рівняння авторегресії й перевірити гіпотезу за критерієм Стьюдента. Але, як ми вже відзначали, процедура тестування, що базується на застосуванні методу найменших квадратів, до нестаціонарного ряду (а Процедура тестування повинна базуватися на такій моделі, що буде стаціонарний при прийнятті Дикі й Фулер запропонували прийнятний і простий метод тестування
де [дійсно: І строго говорячи, DF-Тест у якості
Звідси його назва - unit root test - тест на одиничний корінь. Рівняння (3) може бути представлене ще в такий спосіб:
Якщо в рівнянні (2) Тест DF складається в перевірці заперечності Якщо В силу емпіричного скоріше, ніж теоретичного, характеру таблиць, вони містять елемент невизначеності – дається не одне, а два теоретичні значення – верхнє й нижнє. Якщо розрахункове значення Тест Дикі-Фулера може бути використаний для перевірки стаціонарності процесів, породжених випадковим блуканням із дрейфом, тобто шляхом перевірки рівняння:
Техніка перевірки аналогічна. Еквівалентне (4) рівняння:
Але з обліком того, що розподіл t-статистики для Ще одна модифікація рівняння DF - включення лінійного детермінованого тренда.
або Це рівняння дозволяє перевірити відсутність стохастичного тренда ( Отже, якщо · · ·
ü Якщо дані генеруються відповідно до процесу ü Якщо дані отримані згідно ü Якщо дані генеруються процесом Якщо є підстави припускати, що розглянута змінна нестаціонарна й має тренд, то почати тестування рекомендується з регресії Недолік тесту DF полягає в тім, що тест Дикі-Фулера має обмеження: 1. Припущення про те, що змінна треба авторегресійному процесу першого порядку; 2. Помилки Дикі й Фулер запропонували використовувати в якості додаткових (екзогенних змінних) регресорів змінну в лівій частині рівняння, узяту з різними лагами (лаги першої різниці). Модифікований тест DF передбачає авторегресійні процеси більше високих порядків і зветься додаткового (розширеного) тесту Дикі-Фулера (AFD – augment Dickey-Fuller test). Базові рівняння приймають наступний вид:
Додаткова авторегресійна компонента вводиться для того, щоб забрати автокореляцію залишків, до якої чутливий DF-Тест. Розподіл тестів для цих рівнянь асимптотично збігаються з відповідними тестами DF і використовують ті ж таблиці.
|

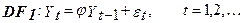 (2)
(2)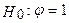 .
.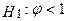 .
.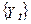 нестаціонарений будучи випадковим блуканням. Відповідно до альтернативної гіпотези,
нестаціонарений будучи випадковим блуканням. Відповідно до альтернативної гіпотези, 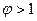 не розглядається.
не розглядається.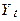 нестаціонарений, якщо
нестаціонарений, якщо 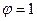 ), може вводити в оману, показуючи значимість фактора в той час, як він таким не є.
), може вводити в оману, показуючи значимість фактора в той час, як він таким не є.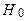 .
.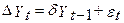 (3)
(3)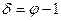
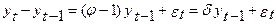 ].
].
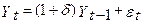
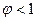 , то в рівнянні (3)
, то в рівнянні (3) 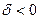 (негативно) – означає стаціонарність процесу.
(негативно) – означає стаціонарність процесу.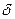 . Відхилення нульової гіпотези (
. Відхилення нульової гіпотези (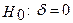 ) на користь альтернативної (
) на користь альтернативної (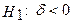 ) означає, що
) означає, що 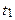 -статистика має нестандартний розподіл. Для її використання потрібні спеціальні таблиці. Такі таблиці були отримані емпірично, з використанням методу Монте-Карло. За основу був узятий процес AR(1) с.
-статистика має нестандартний розподіл. Для її використання потрібні спеціальні таблиці. Такі таблиці були отримані емпірично, з використанням методу Монте-Карло. За основу був узятий процес AR(1) с. 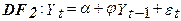 (4)
(4)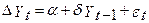
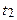 - в основі лежить процес випадкового блукання із дрейфом, використовуються інші критичні значення.
- в основі лежить процес випадкового блукання із дрейфом, використовуються інші критичні значення. (5)
(5)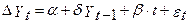
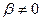 ). Для цього тесту складені свої таблиці критичних значень -
). Для цього тесту складені свої таблиці критичних значень - 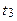 .
.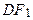 (2) – стаціонарний процес AR(1) з нульовим середнім,
(2) – стаціонарний процес AR(1) з нульовим середнім,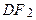 (4) – стаціонарний процес AR(1) із середнім
(4) – стаціонарний процес AR(1) із середнім 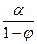 ,
,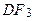 (5) – стаціонарний процес AR(1) навколо лінійного тренда, якщо
(5) – стаціонарний процес AR(1) навколо лінійного тренда, якщо 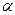 , тоді
, тоді 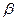 , то
, то  нескорельовані.
нескорельовані.