Модель випадкового блукання із дрейфом
Тепер допустимо, що зміни в Y частково детерміновані й частково стохастичні. Модель випадкового блукання із дрейфом виходить (перетвориться) з моделі випадкового блукання додаванням константи
Якщо дано початкове значення
Тут поводження Якщо ми візьмемо математичне очікування, середнє значення Помітимо, що перша різниця ряду стаціонарна; перехід до першої різниці створює стаціонарну послідовність Ясно, що динаміку тимчасового ряду визначає детермінований тренд. У дуже більших вибірках, асимптотична теорія припускає, що це, у всякому разі, має місце. Однак не слід думати, що завжди легко (розпізнати) розрізнити модель випадкового блукання й модель випадкового блукання із дрейфом. У малих вибірках, збільшення дисперсії ФУНКЦІЯ ПРОГНОЗУВАННЯ Замінимо в (4) t на t+S:
Взявши умовне математичне очікування від
По контрасту із чистою моделлю випадкового блукання, що прогнозує функція не є категорична пряма. Той факт, що середня зміна в
|

 :
: (3)
(3)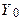 , загальне рішення для
, загальне рішення для 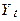 буде:
буде: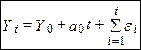 (4)
(4)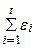 .
. , а середнє значення
, а середнє значення 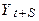 дорівнює
дорівнює  (це треба з того, що
(це треба з того, що  )
) .
.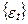 або зменшення абсолютного значення
або зменшення абсолютного значення 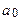 може перекривати довгострокові властивості послідовності. Помітимо, що багато рядів – включаючи пропозицію грошей і реальний ВНП (GNP ) – поводяться як модель випадкового блукання із дрейфом.
може перекривати довгострокові властивості послідовності. Помітимо, що багато рядів – включаючи пропозицію грошей і реальний ВНП (GNP ) – поводяться як модель випадкового блукання із дрейфом.
 , відбивається на прогнозі. До того ж взявши
, відбивається на прогнозі. До того ж взявши 


