Модель випадкового пошуку
Розглянемо модель
що є часткою случаємо AR(1)-процесу ( Якщо
взявши математичні очікування, ми одержуємо:
т.п. середнє значення випадкового блукання дорівнює константі. Однак всі стохастичні зміни (перегони) мають неослабний вплив на послідовність
Аналогічно, умовне математичне очікування
так що
Умовний математичні очікування для всіх значень Однак коливання (перегони)
Тому
Т.к. дисперсія – не константа ( Отже, випадкове блукання «ізвивається», «бродить» без якої-небудь явної тенденції до збільшення (росту) або зниженню. Цікаво розглядати коваріациею між
Таким чином, коефіцієнт кореляції дорівнює:
Цей результат відіграє важливу роль у дослідженні нестаціонарних рядів. Для невеликих значень Таким чином, неможливо використовувати автокореляційну функцію для диференціації процесів з одиничним коренем (
|

 , (1)
, (1)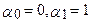 ).
).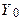 - відома початкова умова, загальне рішення рівняння може бути представлене у вигляді так званої моделі випадкового блукання (random walk model)
- відома початкова умова, загальне рішення рівняння може бути представлене у вигляді так званої моделі випадкового блукання (random walk model)
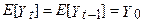
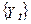 . Якщо відомі перші t реалізацій процесу (послідовності)
. Якщо відомі перші t реалізацій процесу (послідовності) 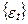 , умовне математичне очікування
, умовне математичне очікування  дорівнює
дорівнює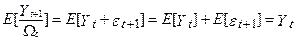
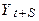 (для будь-яких S>0)
(для будь-яких S>0)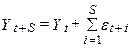
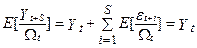
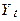 .
. (мають) впливають на послідовність
(мають) впливають на послідовність 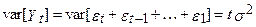
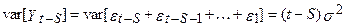 .
. ), процес випадкового блукання (не є стаціонарним) нестаціонарні. Більше того, при
), процес випадкового блукання (не є стаціонарним) нестаціонарні. Більше того, при 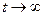 , дисперсія
, дисперсія 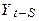 . Тому що середнє значення - константа, можна записати:
. Тому що середнє значення - константа, можна записати: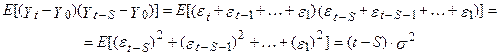
 (2)
(2)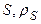 приблизно дорівнює 1. У міру збільшення S значення
приблизно дорівнює 1. У міру збільшення S значення  повільно зменшується, отже, у вибіркових даних, автокореляційна функція процесу випадкового блукання має слабку тенденцію до загасання.
повільно зменшується, отже, у вибіркових даних, автокореляційна функція процесу випадкового блукання має слабку тенденцію до загасання.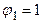 ) і процесів, у яких
) і процесів, у яких  близько до одиниці.
близько до одиниці.


