У моделі випадкового блукання із шумом 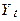 є сума стохастичного тренда й компонента білого шуму. Формально ця третя модель представляється як
є сума стохастичного тренда й компонента білого шуму. Формально ця третя модель представляється як
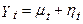 (5)
(5)
 (6)
(6)
де 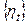 - процес білого шуму з дисперсією рівної
- процес білого шуму з дисперсією рівної 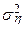 й
й 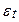 і
і 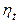 незалежно розподілені для всіх t і S, тобто
незалежно розподілені для всіх t і S, тобто  .
.
Легко перевірити, що послідовність 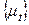 являє собою стохастичний тренд. При відомій початковій умові
являє собою стохастичний тренд. При відомій початковій умові 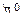 , рішення для
, рішення для 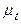 є
є
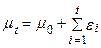
Поєднуючи це вираження з білим шумом, маємо:
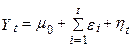
Тепер допустимо, що в момент t=0 значення 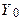 задається
задається 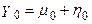 , так що рішення для моделі випадкового блукання із шумом може бути записане як
, так що рішення для моделі випадкового блукання із шумом може бути записане як
 (7)
(7)
Ключові властивості цієї моделі такі:
1. Безумовна середня послідовності 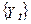 константа:
константа:
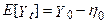
і прогноз на S періодів:
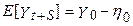
Помітимо, що наступні один за іншим збурювання 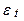 мають постійний вплив на
мають постійний вплив на 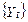 . Отже,
. Отже, 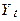 є стохастичний тренд
є стохастичний тренд 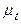 .
.
2. Послідовність  має компоненту чистого шуму, і
має компоненту чистого шуму, і 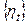 послідовність має тільки тимчасовий ефект із позиції впливу на
послідовність має тільки тимчасовий ефект із позиції впливу на  . Поточна реалізація
. Поточна реалізація 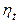 впливає тільки на
впливає тільки на 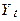 , але не на наступні
, але не на наступні 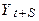 .
.
3. Дисперсія  не постійна:
не постійна:
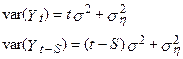
Як і в інших моделях зі стохастичним трендом, дисперсія 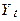 в міру збільшення t росте нескінченно. Наявність компонента білого шуму означає, що коефіцієнт кореляції між
в міру збільшення t росте нескінченно. Наявність компонента білого шуму означає, що коефіцієнт кореляції між 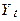 і
і 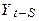 менше, ніж для чистої моделі випадкового блукання.
менше, ніж для чистої моделі випадкового блукання.
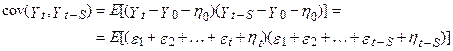
Т.к. 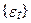 і
і  незалежні послідовності білого шуму,
незалежні послідовності білого шуму,
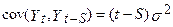
і коефіцієнт кореляції
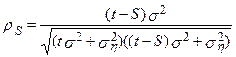
Порівняння з (2) - 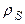 для моделі чисто випадкового блукання – підтверджує, що автокореляції для моделі випадкового блукання із шумом завжди менше для
для моделі чисто випадкового блукання – підтверджує, що автокореляції для моделі випадкового блукання із шумом завжди менше для  .
.
ФУНКЦІЯ ПРОГНОЗУ
Нехай відомі вибіркові значення
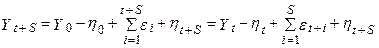
Взявши умовне математичне очікування, одержуємо
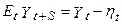
Таким чином, модель випадкового блукання із шумом містить і тренд, і іррегулярний компонент. Звичайно, 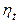 має часовий ефект тільки на
має часовий ефект тільки на 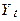 ; прогноз
; прогноз 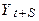 - поточне значення
- поточне значення 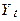 зменшене на
зменшене на 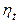 . Постійний компонент
. Постійний компонент 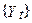 - стохастичний тренд
- стохастичний тренд 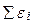 .
.

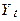 є сума стохастичного тренда й компонента білого шуму. Формально ця третя модель представляється як
є сума стохастичного тренда й компонента білого шуму. Формально ця третя модель представляється як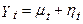 (5)
(5) (6)
(6)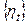 - процес білого шуму з дисперсією рівної
- процес білого шуму з дисперсією рівної 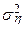 й
й 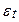 і
і 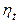 незалежно розподілені для всіх t і S, тобто
незалежно розподілені для всіх t і S, тобто  .
.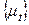 являє собою стохастичний тренд. При відомій початковій умові
являє собою стохастичний тренд. При відомій початковій умові 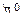 , рішення для
, рішення для 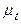 є
є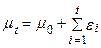
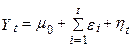
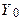 задається
задається 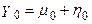 , так що рішення для моделі випадкового блукання із шумом може бути записане як
, так що рішення для моделі випадкового блукання із шумом може бути записане як (7)
(7)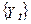 константа:
константа: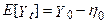
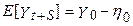
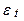 мають постійний вплив на
мають постійний вплив на 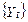 . Отже,
. Отже,  має компоненту чистого шуму, і
має компоненту чистого шуму, і 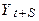 .
.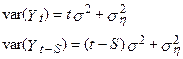
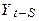 менше, ніж для чистої моделі випадкового блукання.
менше, ніж для чистої моделі випадкового блукання.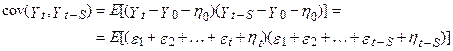
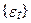 і
і  незалежні послідовності білого шуму,
незалежні послідовності білого шуму,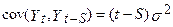
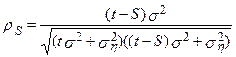
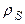 для моделі чисто випадкового блукання – підтверджує, що автокореляції для моделі випадкового блукання із шумом завжди менше для
для моделі чисто випадкового блукання – підтверджує, що автокореляції для моделі випадкового блукання із шумом завжди менше для  .
.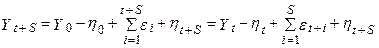
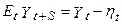
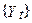 - стохастичний тренд
- стохастичний тренд 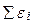 .
.


