Активность и коэффициент активности для различных стандартных состояний
– Задача. Рассчитать коэффициенты активности титана f Ti в расплавах Ni–Тi (стандартное состояние - 1 %-ный раствор) по данным о gTi (стандартное состояние - чистый жидкий титан) при 1800 К. – Исходные данные. Концентрационная зависимость коэффициента активности gTi в расплавах Ni–Тi при 1800 К [2] (таблица). Коэффициенты активности титана в расплавах Ni–Ti при 1800 К
– Теория. Величина термодинамической активности может быть определена только относительно того или иного стандартного состояния. Бессмысленно говорить об активности элемента в растворе без указания его стандартного состояния. Это следует из определения активности как – – Если стандартное состояние, а следовательно, и – Рассмотрим раствор, содержащий компонент i (массовая доля в процентах [% i ], мольная доля хi). При выборе в качестве стандартного состояния 1 %-ного идеального раствора, подчиняющегося закону Генри, активность компонента i равна
– где fi - коэффициент активности компонента i. – Если за стандартное состояние принять чистый элемент i, то
– В данном случае активность обозначается – Учитывая, что [% i ] = (хiMi ×100)/(х 1 M 1 + хiMi), – где Mi и M 1 - атомные массы растворенного элемента i и растворителя, из уравнений (1.7) и (1.8) получим
– Отношение (1.9) не зависит от состава. Для разбавленных растворов ([% i ]® 0, x 1 ® 1, fi = 1, g i =
– Отсюда
что эквивалентно соотношению, полученному К. Люписом [3, с. 24] и [74]. – Решение. Рассчитаем коэффициент активности и активность титана в расплаве Ni–Ti эквиатомного состава (х Ti= х Ni = 0,5):
– Мольной доле х Ti = 0,5 соответствует [% Тi] = 44,9, при этом – – 2. Можно представить гипотетический идеальный раствор, подчиняющийся закону Генри во всей области концентраций. Если концентрацию выразить в мольных долях, то активность компонента i в таком растворе
– следует, что j i = – 3. Для практических расчетов часто используют упрощенное соотношение f i = – вместо выражения (1.10), т.е. считают, что f i = j i. – Уравнение (1.11) дает хорошие результаты при хi ® 0 или М 1» Мi. Для расплава Ni–Тi коэффициент активности f Ti близок к j Ti при х Ti < 0,3. – 4. Температура плавления титана превышает заданную температуру расплава Т = 1800 К, поэтому в качестве стандартного состояния может быть выбран чистый твердый титан. В этом случае
– Учитывая, что
|

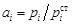 . (1.6)
. (1.6)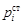 не заданы, то величина ai не может быть определена. Из этого же определения следует, что активность одного и того же элемента при разных стандартных состояниях может иметь значения, отличающиеся на порядок. Ниже будет показано, как можно рассчитать активность элемента в одном стандартном состоянии по данным об активности в другом стандартном состоянии.
не заданы, то величина ai не может быть определена. Из этого же определения следует, что активность одного и того же элемента при разных стандартных состояниях может иметь значения, отличающиеся на порядок. Ниже будет показано, как можно рассчитать активность элемента в одном стандартном состоянии по данным об активности в другом стандартном состоянии.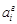 = fi [% i ], (1.7)
= fi [% i ], (1.7)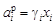 . (1.8)
. (1.8) , так как коэффициент активности g i характеризует отклонение от закона Рауля (
, так как коэффициент активности g i характеризует отклонение от закона Рауля ( ).
). . (1.9)
. (1.9)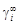 ) оно преобразуется к виду
) оно преобразуется к виду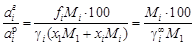 .
.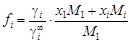 , (1.10)
, (1.10)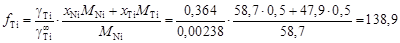 .
.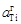 = = f Ti [% Тi] = 138,9 × 44,9 = 6237. Большие значения a Ti являются результатом значительных положительных отклонений от закона Генри. Рассчитанные величины f Ti приведены в таблице,
= = f Ti [% Тi] = 138,9 × 44,9 = 6237. Большие значения a Ti являются результатом значительных положительных отклонений от закона Генри. Рассчитанные величины f Ti приведены в таблице, 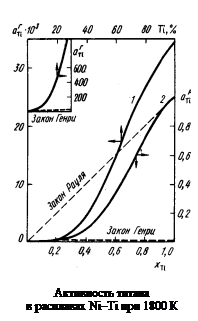 Примечания. 1. Из рисунка следует, что растворы титана в никеле характеризуются отрицательными отклонениями от закона Рауля (gTi < 1) и положительными от закона Генри (f Ti > 1). Видно также, что величина
Примечания. 1. Из рисунка следует, что растворы титана в никеле характеризуются отрицательными отклонениями от закона Рауля (gTi < 1) и положительными от закона Генри (f Ti > 1). Видно также, что величина 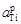 не превышает 1, в то время как
не превышает 1, в то время как  . Величина
. Величина 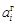 может быть как больше, так и меньше 1, поскольку
может быть как больше, так и меньше 1, поскольку 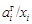 . Из соотношения
. Из соотношения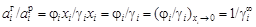
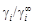 . Рассчитанные значения jTi приведены в таблице.
. Рассчитанные значения jTi приведены в таблице. .
.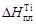 = 18643 Дж/моль,
= 18643 Дж/моль, 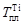 = 1943 К, получим при Т = 1800 К
= 1943 К, получим при Т = 1800 К 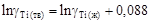 .
.


