Среднюю квадратичную скорость
характеризующую всю совокупность молекул газа. Уравнение (43.1) с уче- том (43.2) примет вид
Учитывая, что п =, получим (43.4) или
где Е — суммарная кинетическая энер- гия поступательного движения всех молекул газа. Так как масса газа
Для 1 моль газа т= М(М— моляр- ная масса), поэтому
где С другой стороны, по уравнению
откуда
(43.6)
Так как ной молекулы, a NA — постоянная Аво- гадро, то из уравнения (43.6) следует, что
Отсюда найдем, что при комнатной температуре молекулы кислорода име- ют среднюю квадратичную скорость 480 м/с, водорода — 1900 м/с. При тем- пературе жидкого гелия те же скорости будут соответственно 40 и 160 м/с. Средняя кинетическая энергия по- ступательного движения одной молеку- лы идеального газа
[использовали формулы (43.5) и (43.7)] пропорциональна термодинамической температуре и зависит только от нее. При предельно низких температурах (близких к 0 К) выражение (43.8) не справедливо, т. е. средняя кинетическая энергия молекул не пропорциональна температуре. Поэтому утверждение о том, что при 0 К прекращается движе- ние молекул газа, некорректно. В насто- ящее время доказано, что даже при 0 К частицы вещества совершают так назы- ваемые нулевые колебания. Таким образом, термодинамическая температура является мерой средней ки- нетической энергии поступательного движения молекул идеального газа, и формула (43.8) раскрывает молекулярно- кинетическое толкование температуры.
|

 (43.2)
(43.2) (43.3)
(43.3) Выражение (43.3) называется ос- новнымуравнениеммолекулярно-ки- нетической теории идеальных газов. Точный расчет с учетом движения мо- лекул по всевозможным направлениям дает ту же формулу.
Выражение (43.3) называется ос- новнымуравнениеммолекулярно-ки- нетической теории идеальных газов. Точный расчет с учетом движения мо- лекул по всевозможным направлениям дает ту же формулу.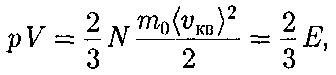 (43.5)
(43.5) то урав- нение (43.4) можно переписать в виде
то урав- нение (43.4) можно переписать в виде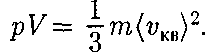
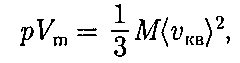
 — молярный объем.
— молярный объем.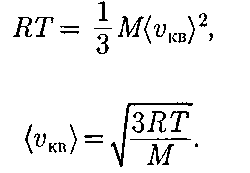 Клапейрона — Менделеева,
Клапейрона — Менделеева,  Таким образом,
Таким образом, — масса од-
— масса од- постоянная Больцмана.
постоянная Больцмана.



