И термодинамический методы. Опытныезаконы идеального газа
ЧАСТЬ 2 ОСНОВЫ МОЛЕКУЛЯРНОЙ ФИЗИКИ И ТЕРМОДИНАМИКИ
Глава 8 МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ ИДЕАЛЬНЫХ ГАЗОВ
§ 41. Статистический и термодинамический методы. Опытныезаконы идеального газа Статистический и термодинамиче- ский методы исследования. Молеку- лярная физика и термодинамика — раз- делы физики, в которых изучаются макроскопические процессы в телах, связанные с огромным числом содержа- щихся в них атомов и молекул. Для ис- следования этих процессов применяют два качественно различных и взаимно дополняющих друг друга метода: ста- тистический (молекулярно-кинети- ческий) и термодинамический. Пер- вый лежит в основе молекулярной фи- зики, второй — термодинамики. Молекулярная физика — раздел физики, в котором изучаются строение и свойства вещества исходя из молеку- лярно-кинетических представлений, основывающихся на том, что все тела состоят из молекул, находящихся в не- прерывном хаотическом движении. Идея об атомном строении вещества высказана древнегреческим философом Демокритом (460 — 370 до п. э.). Атомис- тика возрождается вновь лишь в XVII в. и развивается в работах М.В.Ломоно- сова, взгляды которого на строение ве- щества и тепловые явления были близ- ки к современным. Строгое развитие молекулярной теории относится к се- редине XIX в. и связано с работами не- мецкого физика Р.Клаузиуса (1822 — 1888), Дж. Максвелла и Л.Больцмана. Процессы, изучаемые молекулярной физикой, являются результатом сово- купного действия огромного числа мо- лекул. Законы поведения огромного числа молекул, являясь статистически- ми закономерностями, изучаются с по- мощью статистического метода. Этот метод основан на том, что свой- ства макроскопической системы в ко- нечном счете определяются свойствами частиц системы, особенностями их дви- жения и усредненными значениями ди- намических характеристик этих частиц (скорости, энергии и т.д.) Например, температура тела определяется скоро- стью хаотического движения его моле- кул, но так как в любой момент време- ни разные молекулы имеют различные скорости, то она может быть выражена только через среднее значение скорос- ти движения молекул. Нельзя говорить о температуре одной молекулы. Таким образом, макроскопические характери- стики тел имеют физический смысл лишь в случае большого числа молекул.
Термодинамика — раздел физики, в котором изучаются общие свойства макроскопических систем, находящих- ся в состоянии термодинамического равновесия, и процессы перехода меж- ду этими состояниями. Термодинами- ка не рассматривает микропроцессы, которые лежат в основе этих превраще- ний. Этим термодинамический метод отличается от статистического. Термо- динамика базируется на двух началах — фундаментальных законах, установлен- ных в результате обобщения опыта. Область применения термодинами- ки значительно шире, чем молекуляр- но-кинетической теории, ибо нет таких областей физики и химии, в которых нельзя было бы пользоваться термоди- намическим методом. Однако с другой стороны, термодинамический метод несколько ограничен: термодинамика ничего не говорит о микроскопическом строении вещества, о механизме явле- ний, а лишь устанавливает связи меж- ду макроскопическими свойствами ве- щества. Молекулярно-кинетическая теория и термодинамика взаимно до- полняют друг друга, образуя единое целое, но отличаясь различными мето- дами исследования. Термодинамика имеет дело с тер- модинамической системой — сово- купностью макроскопических тел, ко- торые взаимодействуют и обменивают- ся энергией как между собой, так и с другими телами (внешней средой). Ос- нова термодинамического метода — оп- ределение состояния термодинамичес- кой системы. Состояние системы зада- ется термодинамическими парамет- рами (параметрами состояния) — совокупностью физических величин, характеризующих свойства термодина- мической системы. Обычно в качестве параметров состояния выбирают темпе- ратуру, давление и удельный объем. Температура — одно из основных понятий, играющих важную роль не только в термодинамике, но и в физике в целом. Температура — физическая величина, характеризующая состояние термодинамического равновесия мак- роскопической системы. В соответствии с решением XI Гене- ральной конференции по мерам и весам (1960) в настоящее время можно при- менять только две температурные шка- лы — термодинамическую и Междуна- роднуюпрактическую,градуированные соответственно в Кельвинах (К) и в гра- дусах Цельсия (°С). В Международ- ной практической шкале температу- ра замерзания и кипения воды при дав- лении 1,013*105Па соответственно 0 и 100 °С (реперные точки). Термодинамическая температур- ная шкала определяется по одной ре- перной точке, в качестве которой взята тройная точка воды (температура, при которой лед, вода и насыщенный пар при давлении 609 Па находятся в термодинамическом равновесии). Тем- пература этой точки по термодинами- ческой шкале равна 273,16 К (точно). Градус Цельсия равен кельвину. В тер- модинамической шкале температура за- мерзания воды равна 273,15 К (при том же давлении, что и в Международной практической шкале), поэтому, по оп- ределению, термодинамическая темпе- ратура и температура по Международ- ной практической шкале связаны соот- ношением Г= 273,15 + t Температура Т= 0 К называется ну- лем кельвин. Анализ различных про- цессов показывает, что 0 К недостижим, хотя приближение к нему сколь угодно близко возможно. Удельный объем v — это объем еди- ницы массы. Когда тело однородно, т. е.
Так как при постоянной массе удель- ный объем пропорционален общему объему, то макроскопические свойства однородного тела можно характеризо- вать объемом тела. Параметры состояния системы мо- гут изменяться. Любое изменение в тер- модинамической системе, связанное с изменением хотя бы одного из ее тер- модинамических параметров, называет- ся термодинамическим процессом. Макроскопическая система находится в термодинамическом равновесии, если ее состояние с течением времени не меняется (предполагается, что вне- шние условия рассматриваемой систе- мы при этом не изменяются). В молекулярно-кинетической тео- рии пользуются идеализированной мо- делью идеального газа,согласно кото- рой считают, что: 1) собственный объем молекул газа пренебрежимо мал по сравнению с объемом сосуда; 2) между молекулами газа отсут- ствуют силы взаимодействия; 3) столкновения молекул газа меж- ду собой и со стенками сосуда абсолют- но упругие. Наиболее близко свойствам идеаль- ного газа соответствуют достаточно раз- реженные газы. Модель идеального газа можно использовать также при изучении реальных газов, так как они в условиях, близких к нормальным (например, водо- род и гелий), а также при низких давле- ниях и высоких температурах близки по
Закон Бойля — Мариотта1: для данной массы газа при постоянной тем- пературе произведение давления газа на его объем есть величина постоянная:
График зависимости между пара- метрами состояния газа при постоян- ной температуре называется изотер- мой. Изотермы в координатах р, V пред- ставляют собой гиперболы, располо- женные на графике тем выше, чем выше температура, при которой происходит процесс (рис. 62). Законы Гей-Люссака2:1) объем дан- ной массы газа при постоянном давлении изменяется линейно с температурой:
2) давление данной массы газа при постоянном объеме изменяется линей- но с температурой:
В этих уравнениях t — температу- ра по шкале Цельсия, р0 и Vo — давле- ние и объем при 0°С, коэффициент
своим свойствам к идеальному газу. Кро- 1/273,15 К. ме того, внеся поправки, учитывающие собственный объем молекул газа и дей- ствующие молекулярные силы, можно перейти к теории реальных газов. Рассмотрим законы, описывающие поведение идеальных газов. Процесс, протекающий при посто- янном давлении, называется изобар-
1 Р. Бойль (1627 —1691) — английский ученый; Э. Мариотт (1620 — 1684) — французский физик. 2 Ж.Гей-Люссак (1778-1850) - француз- ский ученый.
Рис. 64 ным. На диаграмме в координатах V, t (рис. 63) этот процесс изображается прямой,называемой изобарой.Процесс, протекающий при постоянном объеме, называется изохорным. На диаграмме в координатах р, t (рис. 64) он изобража- Закон 1 моль любого газа при одинаковых температуре и давле- нии занимает одинаковый объем. При нормальных условиях этот объем равен 22,41 •
ется прямой, называемой изохорой. P = Pl + P2 +...+ Рп- Из (41.2) и (41.3) следует, что изо- бары и изохоры пересекают ось темпе- ратур в точке t= а определяемой из условия 1 + at = 0. Если перенести начало отсчета в эту точку, то происходит переход к шкале Кельвина (см. рис. 64), откуда
(41.4)
где индексы 1 и 2 относятся к произ- вольным состояниям, лежащим на од- ной изобаре или изохоре. Парциальное давление — давление, которое производил бы газ, входящий в состав газовой смеси, если бы он один занимал объем, равный объему смеси при той же температуре.
§ 42. Уравнение Клапейрона—Менделеева
Как уже указывалось, состояние не- которой массы газа определяется тре- мя термодинамическими параметрами: давлением р, объемом V и температу- рой Т. Между этими параметрами су- ществует определенная связь, называ- емая уравнением состояния, которое в общем виде задается выражением
где каждая из переменных является функцией двух других. Французский физик и инженер Б. Клапейрон (1799 — 1864) вывел урав- нение состояния идеального газа, объе-
1 А.Авогадро (1776—1856) — итальянский физик и химик. 2 Дж.Дальтон (1766—1844) — английский химик и физик.
Переход из состояния 1 в состояние 2 осуществляется в виде двух процессов: 1) изотермического (изотерма 1—1'), 2) изохорного (изохора 1'—2). В соответствии с законами Бойля — Мариотта (41.1) и Гей-Люссака (41.5) запишем:
Исключив из уравнений (42.1) и (42.2)
 Так как состояния 1 и 2 были выб- раны произвольно, то для данной мас- сы газа величина остается посто- янной, т.е. Так как состояния 1 и 2 были выб- раны произвольно, то для данной мас- сы газа величина остается посто- янной, т.е.
Русский ученый Д.И.Менделеев (1834—1907) объединил уравнение Клапейрона с законом Авогадро, отне- ся уравнение (42.3) к 1 моль газа, ис- пользовав молярный объем
удовлетворяет лишь идеальный газ, и оно является уравнением состояния иде- ального газа, называемым также урав- нением Клапейрона—Менделеева.
= 22,41 *
От уравнения (42.4) для 1 моль газа можно перейти к уравнению Клапейро- на—Менделеева для произвольной массы газа. Если при некоторых задан- ных давлении и температуре 1 моль газа занимает молярный объем Vm, то при тех же условиях масса т газа займет объем Менделеева для массы т газа
Выражение (42.3) является уравне- нием Клапейрона, в котором В — газо- вая постоянная, различная для разных газов.
где — количество вещества. Часто пользуются несколько иной формой записи уравнения состояния идеального газа, вводя постоянную Больцмана:
где = п — концентрация молекул (число молекул в единице объема). Таким образом, из уравнения р = пкТ (42.6) следует, что давление идеального газа при данной температуре пропорцио- нально концентрации его молекул (или плотности газа). При одинаковых тем- пературе и давлении все газы содержат в единице объема одинаковое число молекул. Число молекул, содержащих- ся в 1 м3 газа при нормальных условиях, называется числом Лошмидта1:
§ 43. Основное уравнение молекулярно-кинетической теории идеальных газов
Для вывода основного уравнения молекулярно-кинетической теории рассмотрим одноатомный идеальный газ. Молекулы газа движутся хаотичес- ки, число взаимных столкновений меж- ду молекулами газа пренебрежимо мало по сравнению с числом ударов о стенки сосуда, а соударения молекул со стенка- ми сосуда абсолютно упругие. Выделим на стенке сосуда некоторую элементар- ную площадку
1 И.Лошмидт (1821 — 1895) — австрийский химик и физик.
жущаяся перпендикулярно площадке, передает ей импульс
Необходимо, однако, учитывать, что реально молекулы движутся к площад- ке, будет
Тогда давление газа, оказываемое им на стенку сосуда,
|

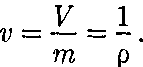 его плотность р = const, то
его плотность р = const, то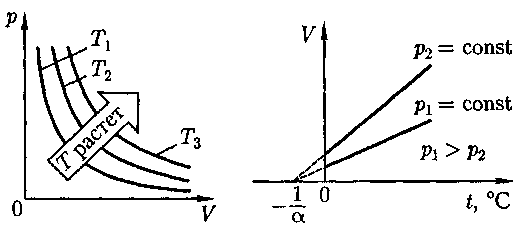 Рис. 62 Рис. 63
Рис. 62 Рис. 63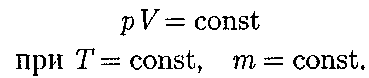 (41.1)
(41.1)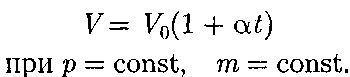 (41.2)
(41.2)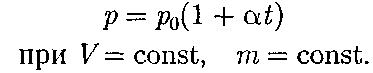 (41.3)
(41.3) -1
-1
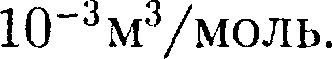
 По определению, 1 моль различных веществ содержит одно и то же число молекул, называемое постоянной Аво- гадро:
По определению, 1 моль различных веществ содержит одно и то же число молекул, называемое постоянной Аво- гадро:
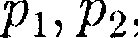
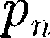 Закон Дальтона2: давление смеси идеальных газов равно сумме парциаль- ных давлений..., входящих в нее газов:
Закон Дальтона2: давление смеси идеальных газов равно сумме парциаль- ных давлений..., входящих в нее газов: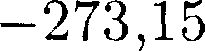 °С,
°С,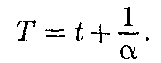
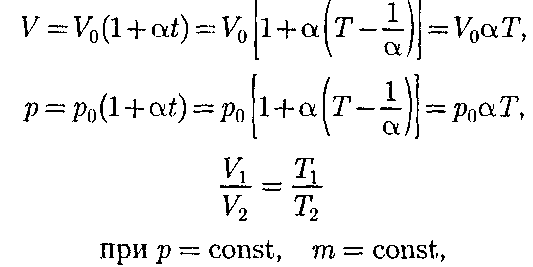 Вводя в формулы
Вводя в формулы  и
и 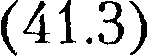 тер- модинамическую температуру, законам Гей-Люссака можно придать более удобный вид:
тер- модинамическую температуру, законам Гей-Люссака можно придать более удобный вид: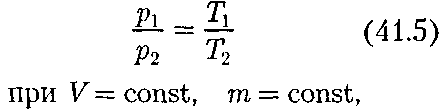

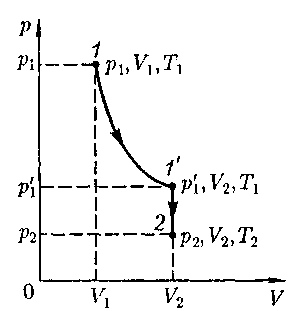 Рис. 65
Рис. 65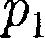 динив законы Бойля — Мариотта и Гей- Люссака. Пусть некоторая масса газа за- нимает объем
динив законы Бойля — Мариотта и Гей- Люссака. Пусть некоторая масса газа за- нимает объем  имеет давление и находится при температуре
имеет давление и находится при температуре  Эта же масса газа в другом произвольном со- стоянии характеризуется параметрами
Эта же масса газа в другом произвольном со- стоянии характеризуется параметрами  (рис. 65).
(рис. 65). (42.1)
(42.1) (42.2)
(42.2) получим
получим
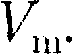 Соглас- но закону Авогадро, при одинаковых р и Т молярные объемы
Соглас- но закону Авогадро, при одинаковых р и Т молярные объемы  различных газов одинаковы, поэтому постоянная В будет одинаковой для всех газов. Эта общая для всех газов постоянная обо- значается R и называется молярной газовой постоянной. Уравнению
различных газов одинаковы, поэтому постоянная В будет одинаковой для всех газов. Эта общая для всех газов постоянная обо- значается R и называется молярной газовой постоянной. Уравнению (42.4)
(42.4)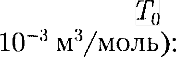 Числовое значение молярной газо- вой постоянной определим из форму- лы (42.4), полагая, что 1 моль газа на- ходится при нормальных условиях
Числовое значение молярной газо- вой постоянной определим из форму- лы (42.4), полагая, что 1 моль газа на- ходится при нормальных условиях  1,013 • 105Па, = 273,15 К,
1,013 • 105Па, = 273,15 К,  =
= - 8,31
- 8,31  • К).
• К).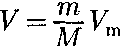 , где М— молярная мас - са (масса 1 моль вещества). Единица молярной массы — килограмм на моль (кг/моль). Уравнение Клапейрона —
, где М— молярная мас - са (масса 1 моль вещества). Единица молярной массы — килограмм на моль (кг/моль). Уравнение Клапейрона — (42.5)
(42.5)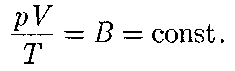 (42.3)
(42.3)
 Исходя из этого уравнение состоя- ния (42.4) запишем в виде
Исходя из этого уравнение состоя- ния (42.4) запишем в виде
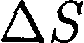 (рис. 66) и вычислим давление, оказываемое на эту площадку. При каждом соударении молекула, дви-
(рис. 66) и вычислим давление, оказываемое на эту площадку. При каждом соударении молекула, дви-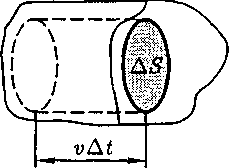 Рис.66
Рис.66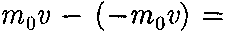
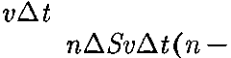
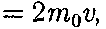 где
где 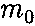 — масса молекулы, v — ее скорость. За время
— масса молекулы, v — ее скорость. За время 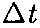 площадки
площадки 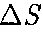 до- стигнут только те молекулы, которые заключены в объеме цилиндра с основа- нием
до- стигнут только те молекулы, которые заключены в объеме цилиндра с основа- нием 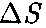 и высотой (см. рис. 66). Число этих молекул равно концентрация молекул).
и высотой (см. рис. 66). Число этих молекул равно концентрация молекул). подразными углами, имеют раз-личные скорости, причем скорость мо- лекул при каждом соударении меняет- ся. Для упрощения расчетов хаотиче- ское движение молекул заменяют дви- жением вдоль трех взаимно перпенди- кулярных направлений, так что в лю- бой момент времени вдоль каждого из них движется 1/3 молекул, причем из них половина (l/б) движется вдоль дан- ного направления в одну сторону, по- ловина — в противоположную. Тогда число ударов молекул, движущихся в заданном направлении, о площадку
подразными углами, имеют раз-личные скорости, причем скорость мо- лекул при каждом соударении меняет- ся. Для упрощения расчетов хаотиче- ское движение молекул заменяют дви- жением вдоль трех взаимно перпенди- кулярных направлений, так что в лю- бой момент времени вдоль каждого из них движется 1/3 молекул, причем из них половина (l/б) движется вдоль дан- ного направления в одну сторону, по- ловина — в противоположную. Тогда число ударов молекул, движущихся в заданном направлении, о площадку 
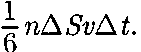 При столкновении с площадкой эти молекулы передадут ей импульс
При столкновении с площадкой эти молекулы передадут ей импульс
 (43.1)
(43.1)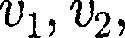 Если газ в объеме V содержит N мо- лекул, движущихся со скоростями
Если газ в объеме V содержит N мо- лекул, движущихся со скоростями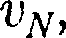 ..., то целесообразно рассматривать
..., то целесообразно рассматривать


