Для рассмотрения конкретных про- цессов найдем в общем виде внешнюю работу, совершаемую газом при изме- нении его объема. Рассмотрим, напри- мер, газ, находящийся под поршнем в цилиндрическом сосуде (рис. 80). Если газ, расширяясь, передвигает поршень на бесконечно малое расстояние dl, то производит над ним работу
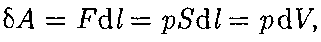
где S — площадь поршня; Sdl — dV — изменение объема системы.
Таким образом,
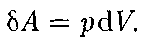 (52.1)
(52.1)
Полную работу А, совершаемую га- зом при изменении его объема от 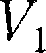 до
до  найдем интегрированием формулы (52.1):
найдем интегрированием формулы (52.1):
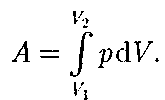 (52.2)
(52.2)
Результат интегрирования опреде- ляется характером зависимости между давлением и объемом газа. Найденное для работы выражение (52.2) справед- ливо при любых изменениях объема твердых, жидких и газообразных тел.
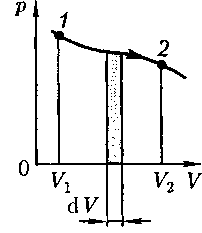 Произведенную при том или ином процессе работу можно изобразить гра- фически с помощью кривой в коорди- натах р, V. Пусть изменение давления
Произведенную при том или ином процессе работу можно изобразить гра- фически с помощью кривой в коорди- натах р, V. Пусть изменение давления

Рис. 80 Рис.81
газа при его расширении изображается кривой на рис. 81. При увеличении объема на  газом рабо- та равна pdV, т.е. определяется площа- дью полоски с основанием
газом рабо- та равна pdV, т.е. определяется площа- дью полоски с основанием 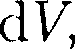 тониро- ванной на рисунке. Поэтому полная ра- бота, совершаемая газом при расшире- нии от объема
тониро- ванной на рисунке. Поэтому полная ра- бота, совершаемая газом при расшире- нии от объема  до объема
до объема 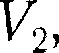 опреде- ляется площадью, ограниченной осью абсцисс, кривой р =
опреде- ляется площадью, ограниченной осью абсцисс, кривой р =  прямыми
прямыми  и
и 
 Графически можно изображать толь- равновесные процессы — процессы, состоящие из последовательности рав- новесных состояний. Они протекают так, что изменение термодинамических параметров за конечный промежуток времени бесконечно мало. Все реальные процессынеравновесны (онипротекают с конечной скоростью), но в ряде слу- чаев неравновесностыо реальных про- цессов можно пренебречь (чем медлен- нее протекает процесс, тем он ближе к равновесному). В дальнейшем рассмат- риваемые процессы будем считать рав-
Графически можно изображать толь- равновесные процессы — процессы, состоящие из последовательности рав- новесных состояний. Они протекают так, что изменение термодинамических параметров за конечный промежуток времени бесконечно мало. Все реальные процессынеравновесны (онипротекают с конечной скоростью), но в ряде слу- чаев неравновесностыо реальных про- цессов можно пренебречь (чем медлен- нее протекает процесс, тем он ближе к равновесному). В дальнейшем рассмат- риваемые процессы будем считать рав-
новесными.
§ 53. Теплоемкость
Удельная теплоемкость вещест- ва — величина, равная количеству теп- лоты, необходимому для нагревания 1 кг вещества на 1 К:
 с
с
Единицей удельной теплоемкости является джоуль па килограмм-кель- вин 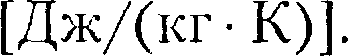
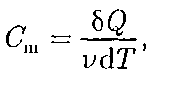 Молярная теплоемкость — вели- чина, равная количеству теплоты, необ- ходимому для нагревания 1 моль веще- ства на 1 К:
Молярная теплоемкость — вели- чина, равная количеству теплоты, необ- ходимому для нагревания 1 моль веще- ства на 1 К:
(53.1)
где У =  — количество вещества.
— количество вещества.
Единица молярной теплоемкости —
джоульнамоль-келъвин [ДжДмоль • К)]. Удельная теплоемкость с связана с мо- лярной  соотношением
соотношением
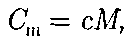 (53.2)
(53.2)
где М — молярная масса вещества.
 Различают теплоемкости при по- стоянном объеме и постоянном давле- нии, если в процессе нагревания веще- ства его объем или давление поддержи- вается
Различают теплоемкости при по- стоянном объеме и постоянном давле- нии, если в процессе нагревания веще- ства его объем или давление поддержи- вается
Запишем выражение первого нача- ла термодинамики 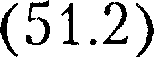 для 1 моль газа с учетом формул (52.1) и (53.1):
для 1 моль газа с учетом формул (52.1) и (53.1):
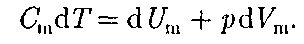 (53.3)
(53.3)
Если газ нагревается при постоян- ном объеме, то работа внешних сил рав- на нулю [см. (52.1)] и сообщаемая газу извне теплота идет только на увеличе- ние его внутренней энергии:
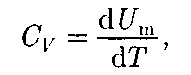 (53.4)
(53.4)
т. е. молярная теплоемкость газа при по- стоянном объеме Су равна изменению внутренней энергии 1 моль газа при по- вышении его температуры на 1 К. Соглас-
но формуле (50.1),  = -RdT, тогда
= -RdT, тогда
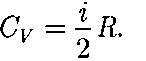 (53.5)
(53.5)
Если газ нагревается при постоян- ном давлении, то выражение (53.3) можно записать в виде
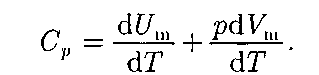
Учитывая, что 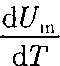 независитотвида процесса (внутренняя энергия идеального газа не зависит ни от р, ни от V, а определяется лишь температу-
независитотвида процесса (внутренняя энергия идеального газа не зависит ни от р, ни от V, а определяется лишь температу-
рой Т) и всегда равна  [см. (53.4)], и дифференцируя уравнение Клапейро- на— Менделеева pVm = RT [см. (42.4)] по Т (р = const), получаем
[см. (53.4)], и дифференцируя уравнение Клапейро- на— Менделеева pVm = RT [см. (42.4)] по Т (р = const), получаем
 (53.6)
(53.6)
Выражение (53.6) называется урав- нением Майера; оно показывает, что 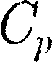 всегда больше
всегда больше  на величину моляр- ной газовой постоянной. Это объясня- ется тем, что при нагревании газа при постоянном давлении требуется еще дополнительное количество теплоты на совершение работы расширения газа, так как постоянство давления обеспе- чивается увеличением объема газа. Ис- пользовав (53.5), выражение (53.6) можно записать в виде
на величину моляр- ной газовой постоянной. Это объясня- ется тем, что при нагревании газа при постоянном давлении требуется еще дополнительное количество теплоты на совершение работы расширения газа, так как постоянство давления обеспе- чивается увеличением объема газа. Ис- пользовав (53.5), выражение (53.6) можно записать в виде
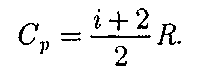 (53.7)
(53.7)
При рассмотрении термодинамиче- ских процессов важно знать характер- ное для каждого газа отношение 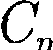

 (53.8)
(53.8)
Из формул (53.5) и (53.7) следует, что молярные теплоемкости определя- ются лишь числом степеней свободы и не зависят от температуры. Это утвер- ждение молекулярно-кинетической те- ории справедливо в довольно широком интервале температур лишь для одно- атомных газов. Уже у двухатомных га- зов число степеней свободы, проявля- ющееся в теплоемкости, зависит от тем-
 82
82 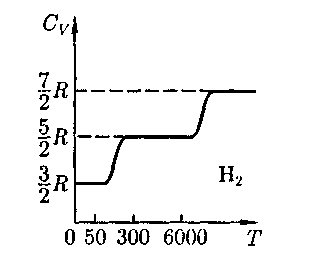
пературы. Молекула двухатомного газа обладает тремя поступательными, дву- мя вращательными и одной колебатель- ной степенями свободы.


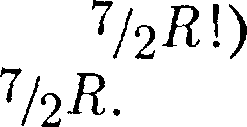 По закону равномерного распреде- ления энергии по степеням свободы (см. § 50), для комнатных температур
По закону равномерного распреде- ления энергии по степеням свободы (см. § 50), для комнатных температур 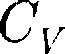 =
= 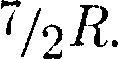 Из качественной экспери- ментальной зависимости молярной теплоемкости водорода (рис. 82) следует, что зависит от температу- ры: при низкой температуре К)
Из качественной экспери- ментальной зависимости молярной теплоемкости водорода (рис. 82) следует, что зависит от температу- ры: при низкой температуре К)  =
= 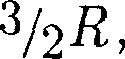 при комнатной — = (вместо расчетных
при комнатной — = (вместо расчетных  очень высокой — Су = Это можно объяс- нить, предположив, что при низких тем- пературах наблюдается только поступа- тельное движение молекул, при ком- натных — добавляется их вращение, а при высоких — к этим двум видам дви- жения добавляются еще колебания мо- лекул.
очень высокой — Су = Это можно объяс- нить, предположив, что при низких тем- пературах наблюдается только поступа- тельное движение молекул, при ком- натных — добавляется их вращение, а при высоких — к этим двум видам дви- жения добавляются еще колебания мо- лекул.
 Расхождение теории и эксперимен- та нетрудно объяснить. Дело в том, что при вычислении теплоемкости надо учитывать квантование энергии враще- ния и колебаний молекул (возможны не любые вращательные и колебатель- ные энергии, а лишь определенный дис- кретный ряд значений энергий). Если энергия теплового движения недоста- точна, например, для возбуждения ко- лебаний, то эти колебания не вносят своего вклада в теплоемкость (соответ- ствующая степень свободы «заморажи- вается» — к ней неприменим закон рав- нораспределения энергии). Этим объясняется, что теплоемкость 1 моль двухатомного газа — водорода — при комнатной температуре равна
Расхождение теории и эксперимен- та нетрудно объяснить. Дело в том, что при вычислении теплоемкости надо учитывать квантование энергии враще- ния и колебаний молекул (возможны не любые вращательные и колебатель- ные энергии, а лишь определенный дис- кретный ряд значений энергий). Если энергия теплового движения недоста- точна, например, для возбуждения ко- лебаний, то эти колебания не вносят своего вклада в теплоемкость (соответ- ствующая степень свободы «заморажи- вается» — к ней неприменим закон рав- нораспределения энергии). Этим объясняется, что теплоемкость 1 моль двухатомного газа — водорода — при комнатной температуре равна 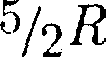
сто 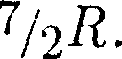 Аналогично можно объяснить уменьшение теплоемкости при низкой температуре («замораживаются» вра- щательные степени свободы) и увели- чение при высокой («возбуждаются» колебательные степени свободы).
Аналогично можно объяснить уменьшение теплоемкости при низкой температуре («замораживаются» вра- щательные степени свободы) и увели- чение при высокой («возбуждаются» колебательные степени свободы).
§ 54. Применение первого начала термодинамики

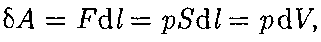
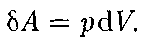 (52.1)
(52.1)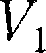 до
до  найдем интегрированием формулы (52.1):
найдем интегрированием формулы (52.1):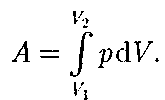 (52.2)
(52.2)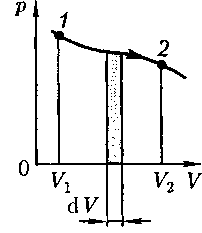 Произведенную при том или ином процессе работу можно изобразить гра- фически с помощью кривой в коорди- натах р, V. Пусть изменение давления
Произведенную при том или ином процессе работу можно изобразить гра- фически с помощью кривой в коорди- натах р, V. Пусть изменение давления
 газом рабо- та равна pdV, т.е. определяется площа- дью полоски с основанием
газом рабо- та равна pdV, т.е. определяется площа- дью полоски с основанием 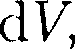 тониро- ванной на рисунке. Поэтому полная ра- бота, совершаемая газом при расшире- нии от объема
тониро- ванной на рисунке. Поэтому полная ра- бота, совершаемая газом при расшире- нии от объема  до объема
до объема 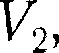 опреде- ляется площадью, ограниченной осью абсцисс, кривой р =
опреде- ляется площадью, ограниченной осью абсцисс, кривой р =  прямыми
прямыми  и
и 
 Графически можно изображать толь- равновесные процессы — процессы, состоящие из последовательности рав- новесных состояний. Они протекают так, что изменение термодинамических параметров за конечный промежуток времени бесконечно мало. Все реальные процессынеравновесны (онипротекают с конечной скоростью), но в ряде слу- чаев неравновесностыо реальных про- цессов можно пренебречь (чем медлен- нее протекает процесс, тем он ближе к равновесному). В дальнейшем рассмат- риваемые процессы будем считать рав-
Графически можно изображать толь- равновесные процессы — процессы, состоящие из последовательности рав- новесных состояний. Они протекают так, что изменение термодинамических параметров за конечный промежуток времени бесконечно мало. Все реальные процессынеравновесны (онипротекают с конечной скоростью), но в ряде слу- чаев неравновесностыо реальных про- цессов можно пренебречь (чем медлен- нее протекает процесс, тем он ближе к равновесному). В дальнейшем рассмат- риваемые процессы будем считать рав- с
с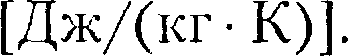
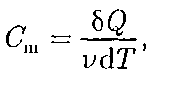 Молярная теплоемкость — вели- чина, равная количеству теплоты, необ- ходимому для нагревания 1 моль веще- ства на 1 К:
Молярная теплоемкость — вели- чина, равная количеству теплоты, необ- ходимому для нагревания 1 моль веще- ства на 1 К: — количество вещества.
— количество вещества. соотношением
соотношением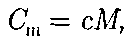 (53.2)
(53.2) Различают теплоемкости при по- стоянном объеме и постоянном давле- нии, если в процессе нагревания веще- ства его объем или давление поддержи- вается
Различают теплоемкости при по- стоянном объеме и постоянном давле- нии, если в процессе нагревания веще- ства его объем или давление поддержи- вается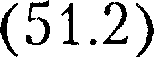 для 1 моль газа с учетом формул (52.1) и (53.1):
для 1 моль газа с учетом формул (52.1) и (53.1):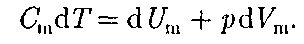 (53.3)
(53.3)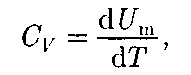 (53.4)
(53.4) = -RdT, тогда
= -RdT, тогда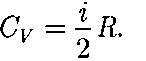 (53.5)
(53.5)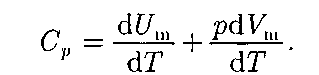
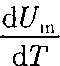 независитотвида процесса (внутренняя энергия идеального газа не зависит ни от р, ни от V, а определяется лишь температу-
независитотвида процесса (внутренняя энергия идеального газа не зависит ни от р, ни от V, а определяется лишь температу- [см. (53.4)], и дифференцируя уравнение Клапейро- на— Менделеева pVm = RT [см. (42.4)] по Т (р = const), получаем
[см. (53.4)], и дифференцируя уравнение Клапейро- на— Менделеева pVm = RT [см. (42.4)] по Т (р = const), получаем (53.6)
(53.6)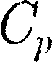 всегда больше
всегда больше  на величину моляр- ной газовой постоянной. Это объясня- ется тем, что при нагревании газа при постоянном давлении требуется еще дополнительное количество теплоты на совершение работы расширения газа, так как постоянство давления обеспе- чивается увеличением объема газа. Ис- пользовав (53.5), выражение (53.6) можно записать в виде
на величину моляр- ной газовой постоянной. Это объясня- ется тем, что при нагревании газа при постоянном давлении требуется еще дополнительное количество теплоты на совершение работы расширения газа, так как постоянство давления обеспе- чивается увеличением объема газа. Ис- пользовав (53.5), выражение (53.6) можно записать в виде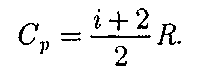 (53.7)
(53.7)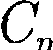

 (53.8)
(53.8) 82
82 


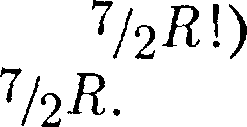 По закону равномерного распреде- ления энергии по степеням свободы (см. § 50), для комнатных температур
По закону равномерного распреде- ления энергии по степеням свободы (см. § 50), для комнатных температур 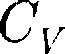 =
= 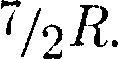 Из качественной экспери- ментальной зависимости молярной теплоемкости водорода (рис. 82) следует, что зависит от температу- ры: при низкой температуре К)
Из качественной экспери- ментальной зависимости молярной теплоемкости водорода (рис. 82) следует, что зависит от температу- ры: при низкой температуре К)  =
= 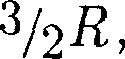 при комнатной — = (вместо расчетных
при комнатной — = (вместо расчетных  очень высокой — Су = Это можно объяс- нить, предположив, что при низких тем- пературах наблюдается только поступа- тельное движение молекул, при ком- натных — добавляется их вращение, а при высоких — к этим двум видам дви- жения добавляются еще колебания мо- лекул.
очень высокой — Су = Это можно объяс- нить, предположив, что при низких тем- пературах наблюдается только поступа- тельное движение молекул, при ком- натных — добавляется их вращение, а при высоких — к этим двум видам дви- жения добавляются еще колебания мо- лекул. Расхождение теории и эксперимен- та нетрудно объяснить. Дело в том, что при вычислении теплоемкости надо учитывать квантование энергии враще- ния и колебаний молекул (возможны не любые вращательные и колебатель- ные энергии, а лишь определенный дис- кретный ряд значений энергий). Если энергия теплового движения недоста- точна, например, для возбуждения ко- лебаний, то эти колебания не вносят своего вклада в теплоемкость (соответ- ствующая степень свободы «заморажи- вается» — к ней неприменим закон рав- нораспределения энергии). Этим объясняется, что теплоемкость 1 моль двухатомного газа — водорода — при комнатной температуре равна
Расхождение теории и эксперимен- та нетрудно объяснить. Дело в том, что при вычислении теплоемкости надо учитывать квантование энергии враще- ния и колебаний молекул (возможны не любые вращательные и колебатель- ные энергии, а лишь определенный дис- кретный ряд значений энергий). Если энергия теплового движения недоста- точна, например, для возбуждения ко- лебаний, то эти колебания не вносят своего вклада в теплоемкость (соответ- ствующая степень свободы «заморажи- вается» — к ней неприменим закон рав- нораспределения энергии). Этим объясняется, что теплоемкость 1 моль двухатомного газа — водорода — при комнатной температуре равна 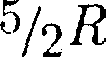
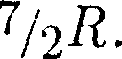 Аналогично можно объяснить уменьшение теплоемкости при низкой температуре («замораживаются» вра- щательные степени свободы) и увели- чение при высокой («возбуждаются» колебательные степени свободы).
Аналогично можно объяснить уменьшение теплоемкости при низкой температуре («замораживаются» вра- щательные степени свободы) и увели- чение при высокой («возбуждаются» колебательные степени свободы).


