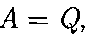Постепеням свободы молекул
Важной характеристикой термоди- намической системы является ее внут- ренняя энергия U — энергия хаотиче- ского (теплового) движения микроча- стиц системы (молекул, атомов, элект- ронов, ядер и т. д.) и энергия взаимодей- ствия этих частиц. Из этого определе- ния следует, что к внутренней энергии не относятся кинетическая энергия
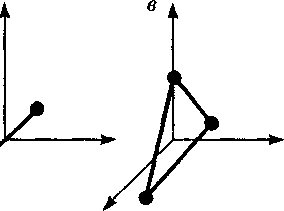
движения системы как целого и потен- циальная энергия системы во внешних полях. Внутренняя энергия — однозначная функция термодинамического состоя- ния системы, т.е. в каждом состоянии система обладает вполне определенной внутренней энергией (она не зависит от того, как система пришла в данное со- стояние). Это означает, что при перехо- де системы из одного состояния в дру- гое изменение внутренней энергии оп- ределяется только разностью значений внутренней энергии этих состояний и не зависит от пути перехода. В § 1 было введено понятие числа степеней свободы: это число независи- мых величин, полностью определяю- щих положение системы в простран- стве. В ряде задач молекулу одноатом- ного газа (рис. 79, а) рассматривают как материальную точку, которой приписы- вают три степени свободы поступатель- ного движения. При этом энергию вра- щательного движения можно не учиты-
В классической механике молекула двухатомного газа в первом приближе- нии рассматривается как совокупность двух материальных точек, жестко свя- занных недеформируемой связью (рис. 79, б). Эта система кроме трех степеней свободы поступательного движения име- ет еще две степени свободы вращатель- ного движения. Вращение вокруг тре- тьей оси (оси, проходящей через оба
Рис. 79 атома) лишено смысла. Таким образом, двухатомный газ обладает пятью степе- нями свободы (i = 5). Трехатомная (рис. 79, в) и много- атомная нелинейные молекулы имеют шесть степеней свободы: три поступа- тельных и три вращательных. Есте- ственно, что жесткой связи между ато- мами не существует. Поэтому для ре- альных молекул необходимо учитывать также степени свободы колебательно- го движения. Независимо от общего числа степе- ней свободы молекул три степени сво- боды всегда поступательные. Ни одна из поступательных степеней свободы не имеет преимущества перед другими, поэтому на каждую из них приходится в среднем одинаковая энергия, равная l/3 значения
В классической статистической фи- зике выводится закон Больцмана о равномерном распределении энергии по степеням свободы молекул: для статистической системы, находящейся в состоянии термодинамического рав- новесия, на каждую поступательную и вращательную степени свободы прихо- дится в среднем кинетическая энергия, равная — ную степень свободы — в среднем энер- гия, равная кТ. Колебательная степень «обладает» вдвое большей энергией потому, что на нее приходится не только кинетическая энергия (как в случае поступательного и вращательного движений), но и по- тенциальная, причем средние значения кинетической и потенциальной энергий одинаковы. Таким образом, средняя энергия молекулы
Следует отметить, что закон Больц- мана является приближенным (полу- чен на основе классических представ- лений о характере движения молекул) и пересмотрен в квантовой статистике. Так как в идеальном газе взаимная потенциальная энергия молекул равна нулю (молекулы между собой не взаи- модействуют), то внутренняя энергия, отнесенная к 1 моль газа, будет равна сумме кинетических энергий кул:
Внутренняя энергия для произволь- ной массы т газа
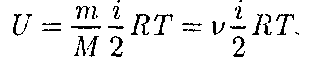
где М — молярная масса; v =
§ 51. Первое начало термодинамики
Рассмотрим термодинамическую систему, для которой механическая энергия постоянна, а изменяется лишь ее внутренняя энергия. Внутренняя энергия системы может изменяться в результате различных процессов, на- пример совершения над системой рабо- ты или сообщения ей теплоты. Так, вдвигая поршень в цилиндр, в котором находится газ, мы сжимаем этот газ, в результате чего его температура повы- шается, т. е. тем самым изменяется (уве- личивается) внутренняя энергия газа. С другой стороны, температуру газа и его внутреннюю энергию можно увели- чить за счет сообщения ему некоторого количества теплоты — энергии, пере- данной системе внешними телами пу- тем теплообмена (процесс обмена внут- ренними энергиями при контакте тел с разными температурами). Таким образом, можно говорить о двух формах передачи энергии от одних тел к другим: работе и теплоте. Энер- гия механического движения может превращаться в энергию теплового дви- жения, и наоборот. При этих превраще- ниях соблюдается закон сохранения и превращения энергии; применительно к термодинамическим процессам этим законом и является первое начало тер- модинамики, установленное в резуль- тате обобщения многовековых опыт- ных данных. Допустим, что некоторая система (газ, заключенный в цилиндр под пор- шнем), обладая внутренней энергией
лоты Q, полученным системой, и рабо- той А, совершенной системой против внешних сил: AU = Q- А,
Уравнение (51.1) выражает первое начало термодинамики: теплота, со- общаемая системе, расходуется на из- менение ее внутренней энергии и на со- вершение ею работы против внешних сил. Выражение (51.1) для элементарно- го процесса можно записать в виде
или в более корректной форме
где Из формулы (51.1) следует, что в СИ количество теплоты выражается в тех же единицах, что работа и энергия, т. е. в джоулях (Дж). Если система периодически воз- вращается в первоначальное состояние, то изменение ее внутренней энергии AU=0. Тогда, согласно первому нача- лу термодинамики,
т. е. вечный двигатель первого рода — периодически действующий двигатель, который совершал бы большую работу, чем сообщенная ему извне энергия, не- возможен (одна из формулировок пер- вого начала термодинамики). § 52. Работа газа
|

 в (43.8):
в (43.8):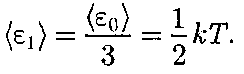
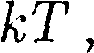 а на каждую колебатель-
а на каждую колебатель-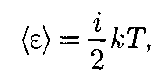
 где — сумма числа поступательных, числа вращательных и удвоенного чис- ла колебательных степеней свободы молекулы:
где — сумма числа поступательных, числа вращательных и удвоенного чис- ла колебательных степеней свободы молекулы: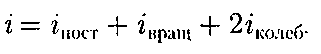
 В классической теории рассматрива- ют молекулы с жесткой связью между атомами; для них совпадает с числом степеней свободы молекулы.
В классической теории рассматрива- ют молекулы с жесткой связью между атомами; для них совпадает с числом степеней свободы молекулы. моле-
моле-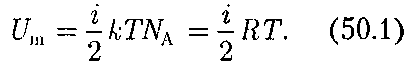
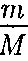 — ко- личество вещества.
— ко- личество вещества.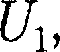 получила некоторое количество тепло- ты Q и, перейдя в новое состояние, ха- рактеризующееся внутренней энергией
получила некоторое количество тепло- ты Q и, перейдя в новое состояние, ха- рактеризующееся внутренней энергией 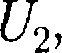 совершила работу А над внешней средой, т. е. против внешних сил. Коли- чество теплоты считается положитель- ным, когда оно подводится к системе, а работа — положительной, когда систе- ма совершает ее против внешних сил. В соответствии с законом сохранения энергии при любом способе перехода системы из первого состояния во вто- рое изменение внутренней энергии AU=
совершила работу А над внешней средой, т. е. против внешних сил. Коли- чество теплоты считается положитель- ным, когда оно подводится к системе, а работа — положительной, когда систе- ма совершает ее против внешних сил. В соответствии с законом сохранения энергии при любом способе перехода системы из первого состояния во вто- рое изменение внутренней энергии AU= 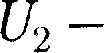
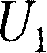 будет одинаковым и рав- ным разности между количеством теп-
будет одинаковым и рав- ным разности между количеством теп-
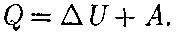 (51.1)
(51.1)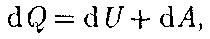
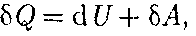 (51.2)
(51.2)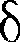 Q — бесконечно малое количество теплоты;
Q — бесконечно малое количество теплоты; 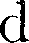 U— бесконечно малое изме- нение внутренней энергии системы; ЬА — элементарная работа. В этом вы- ражении
U— бесконечно малое изме- нение внутренней энергии системы; ЬА — элементарная работа. В этом вы- ражении 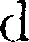 U является полным диффе- ренциалом, а ЬА и
U является полным диффе- ренциалом, а ЬА и 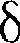 Q таковыми не яв- ляются. В дальнейшем будем использо- вать запись первого начала термодина- мики в форме (51.2).
Q таковыми не яв- ляются. В дальнейшем будем использо- вать запись первого начала термодина- мики в форме (51.2).