Ее статистическое толкование и связь с термодинамической вероятностью
Понятие энтропии введено в 1865 г. Р. Клаузиусом. Для выяснения физи- ческого содержания этого понятия рас- сматривают отношение теплоты Q, по- лученной телом в изотермическом про- цессе, к температуре Т теплоотдающе- го тела, называемое приведенным ко- личеством теплоты. Приведенное количество теплоты, сообщаемое телу на бесконечно малом участке процесса, равно приведенное количество теплоты, сооб- щаемое телу в любом обратимом круго- вом процессе, равно
Из равенства нулю интеграла (57.1), взятого но замкнутому контуру, следу- ет, что подынтегральное выражение — есть полный дифференциал неко- торой функции, которая определяется только состоянием системы и не зави- сит от пути, каким система пришла в это состояние. Таким образом,
Функция состояния, дифференциалом которой является Из формулы (57.1) следует, что для обратимых процессов изменение энтро- пии определяется энтропия, не играет роли, так как физический смысл имеет не сама энтропия, а разность энтропий.
В термодинамике доказывается, что энтропия системы, совершающей нео- братимый цикл, возрастает:
или
Выражения (57.3) и (57.4) относят- ся только к замкнутым системам, если же система обменивается теплотой с внешней средой, то ее энтропия может вести себя любым образом. Соотноше- ния (57.3) и (57.4) можно представить в виде неравенства Клаузиуса
т.е. энтропия замкнутой системы мо- жет либо возрастать (в случае необра- тимых процессов), либо оставаться по- стоянной (в случае обратимых процес- сов). Если система совершает равновес- ный переход из состояния 1 в состоя- ние 2, то, согласно (57.2), изменение эн- тропии
где подынтегральное выражение и пре- делы интегрирования определяются че- рез величины, характеризующие иссле- дуемый процесс. Энтропия определяет- ся с точностью до аддитивной посто- янной. Значение постоянной, с которой
Так как для адиабатного процесса
при изохорном процессе (V1 = V2)
Энтропия обладает свойством адди- тивности: энтропия системы равна сумме энтропий тел, входящих в систе- му. Свойством аддитивности обладают также внутренняя энергия, масса, объем (температура и давление таким свой- ством не обладают).
Более глубокий смысл энтропии вскрывают в статистической физике: энтропия связывается с термодинами- ческой вероятностью состояния системы. Термодинамическая вероятность W состояния системы — это число спосо- бов, которыми может быть реализова- но данное состояние макроскопической системы, или число микросостояний, осуществляющих данное макросостоя- ние [по определению, Согласно Больцману (1872), энтро- пия системы и термодинамическая ве- роятность связаны между собой следу- ющим образом:
где к — постоянная Больцмана. Таким образом, энтропия определя- ется логарифмом числа микросостоя- ний, с помощью которых может быть реализовано данное макросостояние. Следовательно, энтропия может рас- сматриваться какмеравероятности со- стояния термодинамической системы. Формула Больцмана (57.8) позволяет дать энтропии следующее статисти- ческое толкование: энтропия является мерой неупорядоченности системы. В самом деле, чем больше число мик- росостояний, реализующих данное мак- росостояние, тем больше энтропия. В состоянии равновесия — наиболее ве- роятного состояния системы — число микросостояний максимально, при этом максимальна и энтропия. Так как реальные процессы необра- тимы, то можно утверждать, что все процессы в замкнутой системе ведут к увеличению ее энтропии — принцип возрастания энтропии. При статисти- ческом толковании энтропии это озна- чает, что процессы в замкнутой систе- ме идут в направлении увеличения чис- ла микросостояний, иными словами, от менее вероятных состояний к более ве- роятным — до тех пор, пока вероятность состояния не станет максимальной. Сопоставляя выражения (57.5) и (57.8), видим, что энтропия и термоди- намическая вероятность состояний замкнутой системы могут либо возрас- тать (в случае необратимых процессов), либо оставаться постоянными (в случае обратимых процессов). Отметим, однако, что эти утвержде- ния имеют место для систем, состоящих из очень большого числа частиц, но могут нарушаться в системах с малым числом частиц. Для «малых» систем могут наблюдаться флуктуации, т.е. энтропия и термодинамическая вероят- ность состояний замкнутой системы на определенном отрезке времени могут убывать, а не возрастать, или оставать- ся постоянными.
§ 58. Второе начало термодинамики
Первое начало термодинамики, вы- ражая закон сохранения и превращения энергии, не позволяет установить на- правление протекания термодинами- ческих процессов. Кроме того, можно представить процессы, не противореча- щие первому началу, в которых энергия сохраняется, а в природе они не проис- ходят. Появление второго начала тер- модинамики связано с необходимостью дать ответ на вопрос, какие процессы в природе возможны, а какие нет. Второе начало термодинамики определяет на- правление протекания термодинами- ческих процессов. Используя понятие энтропии и не- равенство Клаузиуса (см. § 57), второе начало термодинамики можно сфор-
мулировать как закон возрастания энтропии замкнутой системы при нео- братимых процессах: любой необрати- мый процесс в замкнутой системе про- исходит так, что энтропия системы при этом возрастает. Можно дать более краткую форму- лировку второго начала термодинами- ки: в процессах, происходящих в замкну- той системе, энтропия не убывает. Здесь существенно, что речь идет о зам- кнутых системах, так как в незамкну- тых системах энтропия может вести себя любым образом (убывать, возрас- тать, оставаться постоянной). Кроме того, отметим еще раз, что энтропия остается постоянной в замкнутой сис- теме только при обратимых процессах. При необратимых процессах в замкну- той системе энтропия всегда возра- стает. Формула Больцмана (57.8) позволя- ет объяснить постулируемое вторым началом термодинамики возрастание энтропии в замкнутой системе при нео- братимых процессах: возрастание энт- ропии означает переход системы из ме- неевероятныхвболеевероятныесосто- яния. Таким образом, формула Больц- мана позволяет дать статистическое толкование второго начала термодина- мики. Оно, являясь статистическим за- коном, описывает закономерности ха- отического движения большого числа частиц, составляющих замкнутую сис- тему. Укажем еще две формулировки вто- рого начала термодинамики: 1) по Кельвину: невозможен круго- вой прогресс, единственным результа- том которого является превращение теплоты, полученной от нагревателя, в эквивалентную ей работу; 2) по Клаузиусу:невозможен круго- вой процесс, единственным результа- том которого является передача теп- лоты от менее нагретого тела к более нагретому. Можно довольно просто доказать (предоставим это читателю) эквивален- тность формулировок Кельвина и Кла- узиуса. Кроме того, показано, что если в замкнутой системе провести вообра- жаемый процесс, противоречащий вто- рому началу термодинамики в форму- лировке Клаузиуса, то он сопровожда- ется уменьшением энтропии. Это же доказывает эквивалентность формули- ровки Клаузиуса (а следовательно, и Кельвина) и статистической формули- ровки, согласно которой энтропия зам- кнутой системы не может убывать. В середине XIX в. возникла проблема так называемой тепловой смерти Вселенной. Рассматривая Вселенную как замкнутую систему и применяя к ней второе начало тер- модинамики, Клаузиус свел сто содержание к утверждению, что энтропия РЗселешюй должна достигнуть своего максимума. Это означает, что со временем все формы дви- жения должны перейти в тепловую. Пере- ход же теплоты от горячих тел к холодным приведет к тому, что температура всех тел во Вселенной сравняется, т. с. наступит пол- ное тепловое равновесие и все процессы во Вселенной прекратятся — наступит тепло- вая смерть Вселенной. Ошибочность выво- да о тепловой смерти заключается в том, что бессмысленно применять второе начало тер- модинамики к незамкнутым системам, на- пример к такой безграничной и бесконечно развивающейся системе, как Вселенная. Первое и второе начала термодина- мики дополняются третьим началом термодинамики, или теоремой Нерн-
1 В.Ф.Г.Нернст (1864-1941) - немецкий физик и химик.
§ 59. Тепловые двигатели и холодильные машины.
|

 . Строгий теоретический анализ показывает, что
. Строгий теоретический анализ показывает, что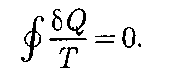 (57.1)
(57.1)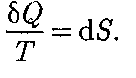 (57.2)
(57.2)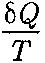 , называется эн- тропией и обозначается S.
, называется эн- тропией и обозначается S.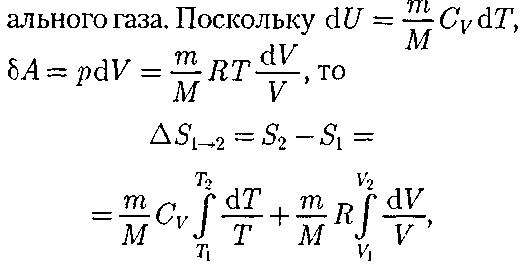 Исходя из выражения (57.6), найдем изменение энтропии в процессах иде-
Исходя из выражения (57.6), найдем изменение энтропии в процессах иде-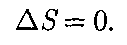 (57.3)
(57.3) (57.4)
(57.4)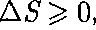 (57.5)
(57.5)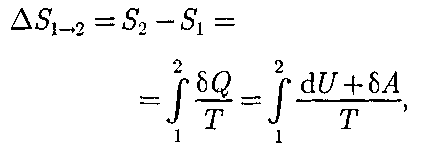 (57.6)
(57.6)
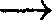 т. е. изменение энтропии
т. е. изменение энтропии 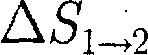 идеаль- ного газа при переходе его из состоя- ния 1 в состояние 2 не зависит от вида процесса перехода 1 2.
идеаль- ного газа при переходе его из состоя- ния 1 в состояние 2 не зависит от вида процесса перехода 1 2. 0, то AS = 0 и, следовательно, S = const, т. е. адиабатный обратимый процесс протекает при постоянной эн- тропии. Поэтому его часто называют изоэнтропийным процессом. Из фор- мулы (57.7) следует, что при изотерми- ческом процессе (
0, то AS = 0 и, следовательно, S = const, т. е. адиабатный обратимый процесс протекает при постоянной эн- тропии. Поэтому его часто называют изоэнтропийным процессом. Из фор- мулы (57.7) следует, что при изотерми- ческом процессе ( =
= 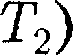

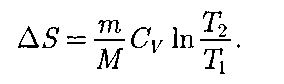
 , т. е. термо- динамическая вероятность не есть ве- роятность в математическом смысле (последняя
, т. е. термо- динамическая вероятность не есть ве- роятность в математическом смысле (последняя  1!)].
1!)].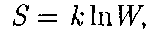 (57.8)
(57.8)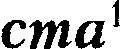 — Планка: энтропия всех тел в со- стоянии равновесия стремится к нулю по мере приближения температуры к нулю кельвин:
— Планка: энтропия всех тел в со- стоянии равновесия стремится к нулю по мере приближения температуры к нулю кельвин:
 Поскольку энтропия определяется с точностью до аддитивной постоянной, то эту постоянную удобно взять равной нулю. Отметим, однако, что это произ- вольное допущение, так как энтропия по своей сущности всегда определяет- ся с точностью до аддитивной постоян- ной. Из теоремы Нернста — Планка сле- дует, что теплоемкости
Поскольку энтропия определяется с точностью до аддитивной постоянной, то эту постоянную удобно взять равной нулю. Отметим, однако, что это произ- вольное допущение, так как энтропия по своей сущности всегда определяет- ся с точностью до аддитивной постоян- ной. Из теоремы Нернста — Планка сле- дует, что теплоемкости 
 при О К равны нулю.
при О К равны нулю.


