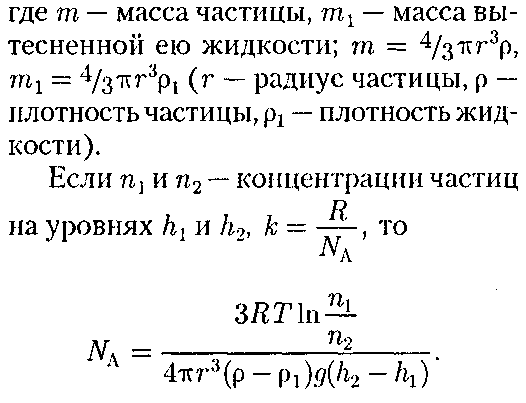И энергиям теплового движения
Молекулы газа совершают хаотичес- кое движение. В результате многократ- ных соударений скорость каждой моле-
Это объясняется тем, что в газе, на- ходящемся в состоянии равновесия, ус- танавливается некоторое стационарное, не меняющееся со временем распреде- ление молекул по скоростям, которое подчиняется вполне определенному статистическому закону. Этот закон те- оретически выведен Дж. Максвеллом (1859). При выводе закона распределения молекул по скоростям считалось, что газ состоит из очень большого числа N тождественных молекул, находящихся в состоянии беспорядочного теплового движения при одинаковой температу- ре. Предполагалось также, что силовые поля на газ не действуют. Закон Максвелла описывается неко- торой
ти будет приходиться некоторое число молекул dN(v), имеющих скорость, зак- люченную в этом интервале. Функция f(v) определяет относительное число (долю) молекул
откуда
Применяя методы теории вероятно- стей, Максвелл нашел функцию f(v) — закон распределения молекул иде- альногогазапоскоростям:
Из (44.1) видно, что конкретный вид функции зависит от рода газа (от мас- сы молекулы) и от параметра состояния (от температуры Т). График функции (44.1) приведен на рис. 67. Так как при возрастании v мно-
Скорость, при которой функция рас- пределения молекул идеального газа по скоростям максимальна, называется наиболее вероятной скоростью. Зна- чение наиболее вероятной скорости можно найти, продифференцировав выражение (44.1) (постоянные множи- тели опускаем) по аргументу v, прирав- няв результат нулю и используя усло- вие для максимума выражения f(v):
Из формулы (44.2) следует, что при повышении температуры максимум функции распределения молекул по скоростям (рис. 68) сместится вправо (значение наиболее вероятной скорос- ти становится больше). Однако пло- щадь, ограниченная кривой, остается неизменной, поэтому при повышении температуры кривая распределения молекул по скоростям будет растяги- ваться и понижаться. Средняя скорость молекулы (v) (средняя арифметическая скорость) определяется по формуле
=
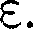  можно найти распределение молекул газа по значениям кинетической энер- гии Для этого перейдем от перемен- ной v кпеременной.Подставив
в (44.4) v и получим
Таким образом, функцияраспреде- ления молекул по энергиям теплово- годвижения
Средняя кинетическая энергия
т. е. получили результат, совпадающий с формулой (43.8).
высотой d/г с основанием площадью 1 м2:
где р — плотность газа на высоте Следовательно,
§ 45. Барометрическая формула. Распределение
При выводе основного уравнения мо- лекулярно-кинетической теории газов и максвелловского распределения моле- кул по скоростям предполагалось, что на молекулы газа внешние силы не действу- (т — масса газа, М
молярная масса ют, поэтому молекулы равномерно рас- пределены по объему. Однако молекулы любого газа находятся в потенциальном поле тяготения Земли. Тяготение, с од- ной стороны, и тепловое движение моле- кул — с другой, приводят к некоторому стационарному состоянию газа, при ко- тором давление газа с высотой убывает. Выведем закон изменения давления с высотой, предполагая, что поле тяго- тения однородно, температура постоян- на и масса всех молекул одинакова. Если атмосферное давление на высоте h равно р (рис. 69), то на высоте h + dh оно равно
Подставив это выражение в (45.1), получим
где р — давление на высоте h. (45.3)
Прибор для определения высоты над земной поверхностью называется высотомером (или альтиметром). Его работа основана на использовании формулы (45.3). Из этой формулы сле- дует, что давление с высотой убывает тем быстрее, чем тяжелее газ. Барометрическую формулу (45.3) можно преобразовать, если воспользо- ваться выражением (42.6)
где mogh — П — потенциальная энергия молекулы в поле тяготения, т. е.
Выражение (45.5) называется рас- пределением Болъцмана для внешне- го потенциального поля. Из него сле- дует, что при постоянной температуре плотность газа больше там, где меньше потенциальная энергия его молекул. Если частицы имеют одинаковую массу и находятся в состоянии хаоти- ческого теплового движения, то распре- деление Больцмана (45.5) справедливо в любом внешнем потенциальном поле, а не только в поле сил тяжести.
§ 46. Среднее число столкновений и средняя длина свободного пробега молекул
Молекулы газа, совершая хаотиче- ское движение, непрерывно сталкива- ются друг с другом. Между двумя пос- ледовательными столкновениями мо- лекулы проходят некоторый путь Минимальное расстояние, на кото- рое сближаются при столкновении цен- тры двух молекул, называется эффек- тивным диаметром молекулы d (рис. 70). Он зависит от скорости сталкива- ющихся молекул, т.е. от температуры газа (несколько уменьшается с ростом температуры). Так как за 1 с молекула проходит в среднем путь, равный средней арифме- тической скорости (v), и если (z) — сред- нее число столкновений, испытывае- мых одной молекулой газа за 1 с, то средняя длина свободного пробега
Для определения (z) представим себе молекулу в виде шарика диамет- ром d, которая движется среди других «застывших» молекул. Эта молекула столкнется только с теми молекулами, центры которых находятся на расстоя- ниях, равных или меньших Среднее число столкновений за 1 с равно числу молекул в объеме «лома- ного» цилиндра:
Рис.70 Рис.71
где п — концентрация молекул; V = = Таким образом, среднее число столкновений
Расчеты показывают, что при учете движения других молекул
Тогда средняя длина свободного пробега
т.е.
§ 47. Опытное обоснование молекулярно-кинетической теории
Рассмотрим некоторые явления, эк- спериментально подтверждающие ос- новные положения и выводы молеку- лярно-кинетической теории. 1. Броуновские движение. Это яв- ление открыто (1827) Броуном1, кото- рый, наблюдая с помощью сильной лупы за взвесью цветочной пыльцы в воде, обнаружил, что частицы пыльцы оживленно и беспорядочно двигались, то вращаясь, то перемещаясь с места на
1 Р.Броун (1773-- 1858) — шотландский бо- таник.
место, подобно пылинкам в солнечном луче. Впоследствии оказалось, что по- добное сложное зигзагообразное дви- жение характерно для любых частиц малых размеров Причина броуновского движения долго оставалась неясной. Лишь через 80 лет после обнаружения этого эффек- та ему было дано объяснение: броунов- ское движение взвешенных частиц вы- зывается ударами молекул среды, в ко- торой частицы взвешены. Так как мо- лекулы движутся хаотически, то броу- новские частицы получают толчки с разных сторон, поэтому и совершают движение столь причудливой формы. Таким образом, броуновское движение является подтверждением выводов мо- лекулярно-кинетической теории о хао- тическом (тепловом) движении атомов и молекул. 2. Опыт Штерна. Первое экспери- ментальное определение скоростей мо- лекул выполнено немецким физиком О.Штерном (1888-1970). Его опыты позволили также оценить распределе- ние молекул по скоростям. Схема установки Штерна представ- лена на рис. 72. Вдоль оси внутреннего цилиндра с щелью натянута платино- вая проволока, покрытая слоем сереб- ра, которая нагревается током при от-
качанном воздухе. При нагревании се- ребро испаряется. Атомы серебра выле- тая через щель, попадают на внутрен- нюю поверхность второго цилиндра, давая изображение щели О. Если при- бор привести во вращение вокруг об- щей оси цилиндров, то атомы серебра осядут не против щели, а сместятся от точки О на некоторое расстояние s. Изображение щели получается размы- тым. Исследуя толщину осажденного слоя, можно оценить распределение молекул по скоростям, которое соответ- ствует максвелловскому распределе- нию. Зная радиусы цилиндров, их угло- вую скорость вращения, а также изме- ряя s, можно вычислить скорость дви- жения атомов серебра при данной тем- пературе проволоки. Результаты опы- та показали, что средняя скорость ато- мов серебра близка к той, которая сле- дует из максвелловского распределения молекул по скоростям. 3. Опыт Ламмерт. Этот опыт позво- ляет более точно определить закон рас- пределения молекул по скоростям. Схе- ма вакуумной установки приведена на рис. 73. Молекулярный пучок, сформи- рованный источником, проходя через щель, попадает в приемник. Между ис- точником и приемником помещают два диска с прорезями, закрепленных на общей оси. При неподвижных дисках молекулы достигают приемника, проходя через прорези в обоих дисках. Если ось при- вести во вращение, то приемника дос- тигнут только те прошедшие прорезь в первом диске молекулы, которые зат- рачивают для пробега между дисками время, равное или кратное времени обо- рота диска. Другие же молекулы задер- живаются вторым диском. Меняя угло- вую скорость вращения дисков и изме- ряя число молекул, попадающих в при- Источник Приемник
4. Опытное определение постоян- нойАвогадро. Воспользовавшись иде- ей распределения молекул по высоте [см. формулу (45.4)], французский уче- ный Ж.Перрен (1870—1942) экспери- ментально определил значение посто- янной Авогадро. Исследуя в микроскоп броуновское движение, он убедился, что броуновские частицы распределя- ются по высоте подобно молекулам газа в поле тяготения. Применив к ним
Значение NA, получаемое из работ Ж. Перрена, соответствовало значени- ям, полученным в других опытах, что
подтверждает применимость к бро- уновским частицам распределения (45.4).
§ 48. Явления переноса в термодинамически
|
кулы изменяется как по модулю, так и по направлению. Однако из-за хаоти- ческого движения молекул все направ- ления движения являются равноверо- ятными, т.е. в любом направлении в среднем движется одинаковое число молекул. По молекулярно-кинетичес- кой теории, как бы ни изменялись ско- рости молекул при столкновениях, сред- няя квадратичная скорость молекул мас- сой в газе, находящемся в состоянии равновесия при (Т= const), остается по- стоянной и равной 
—
называемой фун- кцией распределения молекул по ско- ростям. Если разбить диапазон скоро- стей молекул на малые интервалы, рав- ные dv, то на каждый интервал скорос-
67 
, скорости кото- рых лежат в интервале от v до v + dv, т. е.
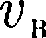чем растет множитель v2, то функция f(v), начинаясь от нуля, достигает мак- симума при и затем асимптотически стремится к нулю. Кривая несиммет-
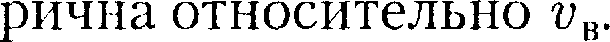Относительное число молекул 
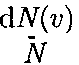скорости которых лежат в интервале от v до v + dv, находится как площадь то- нированной полоски на рис. 67. Смысл этого интеграла в следующем: если про- суммировать все доли молекул, имею- щих всевозможные значения скоростей, то получим единицу. Функция f(v) удовлетворяет условию нормировки
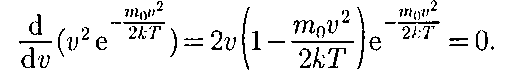
Значения v = 0 и v = ос соответству- ют минимумам выражения (44.1), a значение v, при котором выражение в скобках становится равным нулю, и есть искомая наиболее вероятная ско- рость
(44.2)
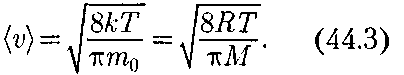Подставляя сюда f(v) и интегрируя, получим
Рис. 68 Скорости, характеризующие сос- тояние газа: 1) наиболее вероятная
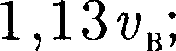3) средняя квадратичная
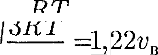/о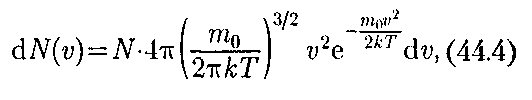
= (см. рис. 67). Ис- ходя из распределения молекул по ско- ростям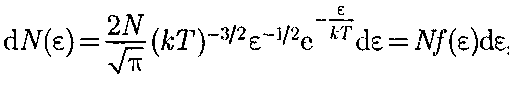
где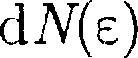 
— число молекул, имеющих кинетическую энергию поступательно- го движения, заключенную в интерва- ле от до е +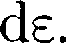 
молекулы идеального газа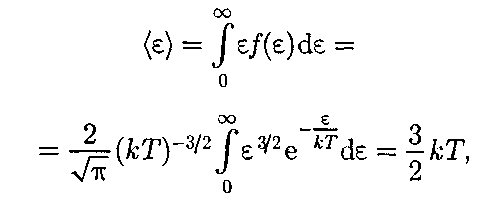
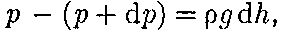
настолько мало, что при изменении высоты в этом пределе плотность газа можно считать постоянной).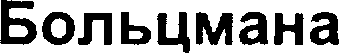
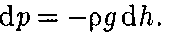(45.1)
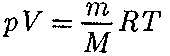Воспользовавшись уравнением со- стояния идеального газа
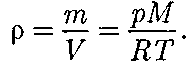газа), находим, что
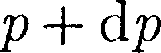(при 
О, так как давление с высотой убывает). Раз- ность давлений р и р + dp равна весу газа, заключенного в объеме цилиндра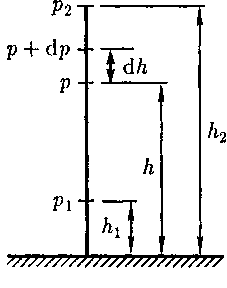
Рис. 69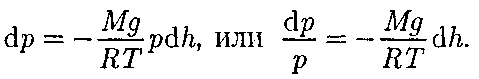
С изменением высоты от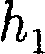 
до 
дав- ление изменяется от •р1 до (см. рис. 
т.е.
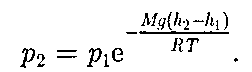(45.2)
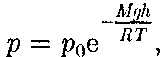Выражение (45.2) называется баро- метрической формулой. Она позволя- ет найти атмосферное давление в зави- симости от высоты или, измерив давле- ние, найти высоту. Так как высоты обо- значаются относительно уровня моря, где давление считается нормальным, то выражение (45.2) может быть записа- но в виде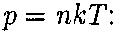
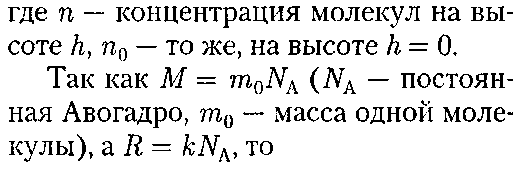
(45.4)
(45.5)
ко- торый называется длиной свободного пробега. В общем случае длина пути между последовательными столкнове- ниями различна, но так как мы имеем дело с огромным числом хаотически движущихся молекул, то можно гово- рить о средней длине свободного про- бега молекул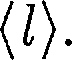 
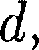т. е. лежат внутри «ломаного» цилиндра радиусом 
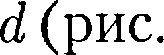71).
((v) — средняя скорость моле- кулы или путь, пройденный ею за 1 с).
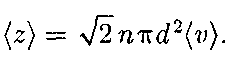
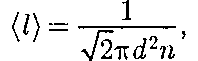
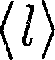обратно пропорциональна кон- центрации п молекул. С другой сторо- ны, из (42.6) следует, что при постоян- ной температуре п пропорциональна давлению р. Следовательно,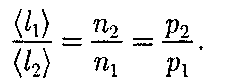
мкм), взвешенных в газе или жидкости. Интенсивность этого движения, названного броунов- ским, повышается с ростом температу- ры среды, с уменьшением вязкости и размеров частиц (независимо от их хи- мической природы).
Рис.72
емник, можно выявить закон распреде- ления молекул по скоростям. Этот опыт также подтвердил справедливость мак- свелловского распределения молекул по скоростям.
распределение, можно записать
